Câu hỏi trong đề: Giải SBT Toán 9 CTST BÀI TẬP CUỐI CHƯƠNG 4 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
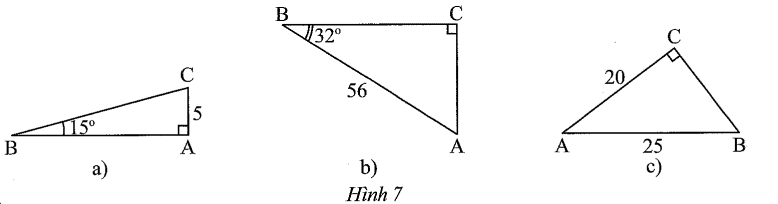
a) Xét tam giác ABC vuông tại A, ta có:
⦁ suy ra
⦁ AB = AC.cotB = 5.cot15° ≈ 18,66;
⦁ AC = BC.sinB, suy ra
b) Xét tam giác ABC vuông tại C, ta có:
⦁ suy ra
⦁ AC = AB.sinB = 56.sin32° ≈ 29,68;
⦁ BC = AB.cosB = 56.cos32° ≈ 47,49.
c) Xét tam giác ABC vuông tại C, ta có:
⦁ AB2 = AC2 + BC2 (định lí Pythagore)
Suy ra
⦁ suy ra
⦁ suy raHot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
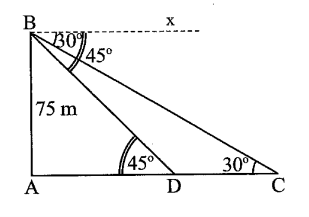
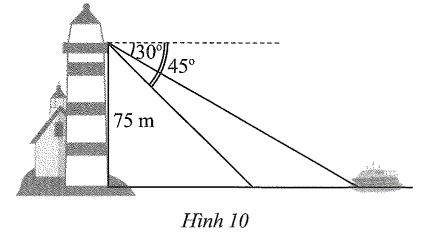
Gọi độ cao từ mắt người đó đến mặt nước biển là AB, suy ra AB = 75 m.
Gọi vị trí chiếc thuyền hướng về phía ngọn hải đăng mà từ trên ngọn tháp quan sát với góc hạ lần lượt là 30° và 45° tương ứng là C, D.
Vì Bx // AD nên và (các cặp góc so le trong).
Xét ∆ABD vuông tại A có suy ra ∆ABD vuông cân tại A.
Do đó AD = AB = 75 m.
Xét ∆ABC vuông tại A, ta có:
Suy ra DC = AC – AD ≈ 129,90 – 75 = 54,90 (m).
Vậy giữa hai lần quan sát, thuyền đi được khoảng 54,90 m.
Lời giải
Đáp án đúng là: B
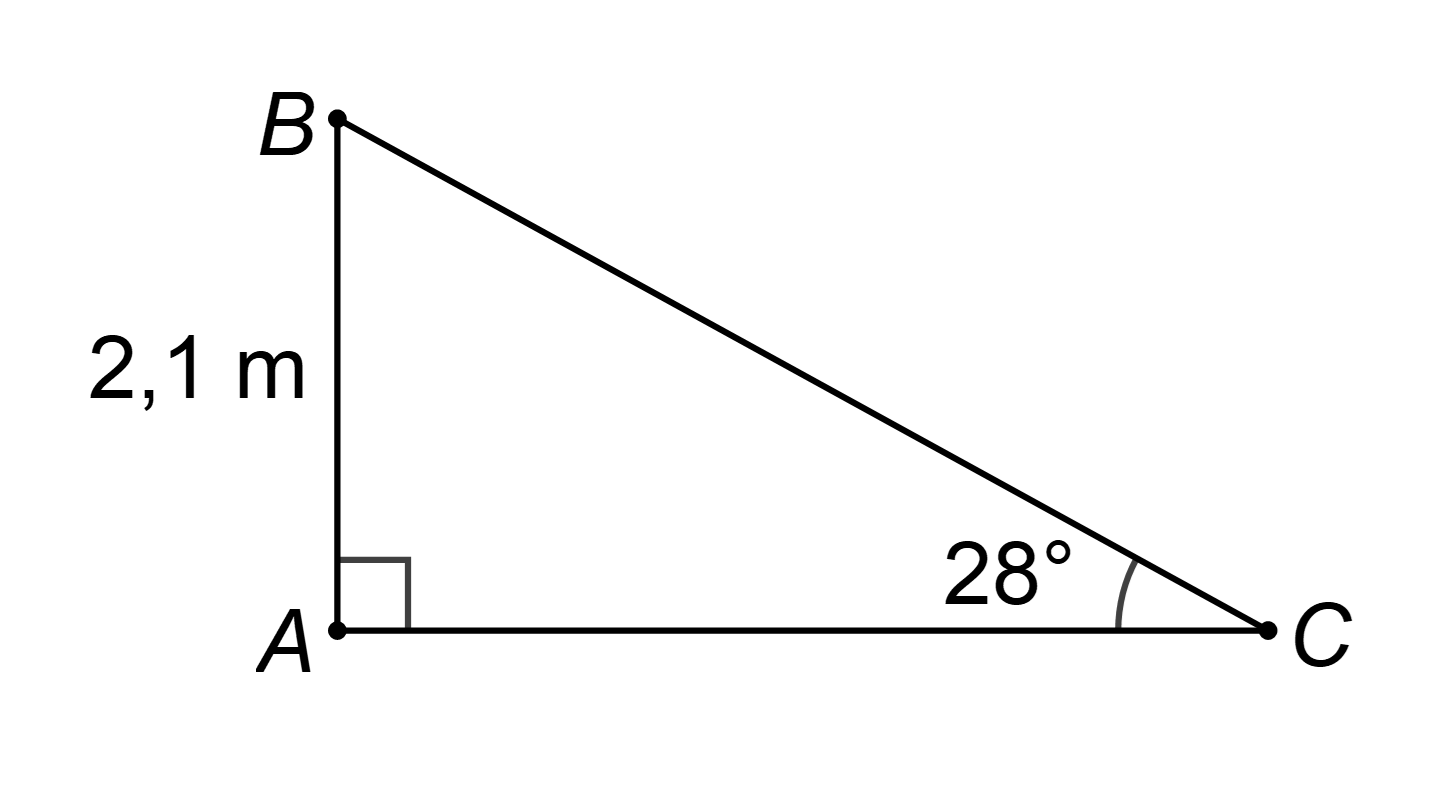
Gọi AB là độ cao của cầu trượt và là độ dốc của cầu trượt.
Khi đó AB = 2,1 m và
Ta có: hay
Suy ra
Vậy độ dài của mặt cầu trượt khoảng 4,5 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập