Cho hình lăng trụ \(ABC.A'B'C'\) có hai đáy là các tam giác đều như hình dưới.
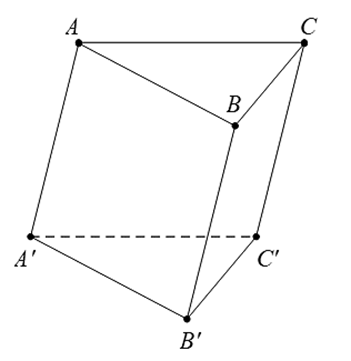
Góc giữa hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {A'C'} \) bằng
Cho hình lăng trụ \(ABC.A'B'C'\) có hai đáy là các tam giác đều như hình dưới.
Góc giữa hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {A'C'} \) bằng
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
Vì \(ABC.A'B'C'\) là hình lăng trụ nên \(\overrightarrow {BC} = \overrightarrow {B'C'} \).
Do đó, \(\left( {\overrightarrow {BC} ,\,\overrightarrow {A'C'} } \right) = \left( {\overrightarrow {B'C'} ,\,\overrightarrow {A'C'} } \right) = 180^\circ - \widehat {B'C'A'}\).
Mà tam giác \(A'B'C'\) đều nên \(\widehat {B'C'A'} = 60^\circ \). Vậy \(\left( {\overrightarrow {BC} ,\,\overrightarrow {A'C'} } \right) = 120^\circ \).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
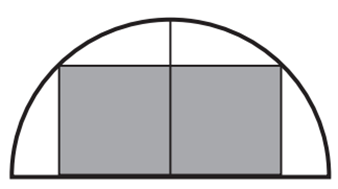
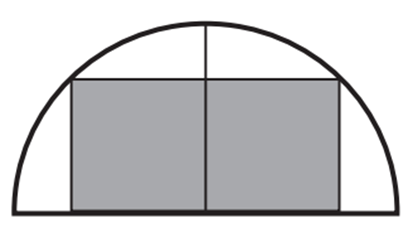
Gọi \(x\,\,\left( {{\rm{cm}}} \right)\) là độ dài một cạnh của tấm giấy hình chữ nhật được cắt ra (cạnh thuộc đường kính) và \(y\,\,\left( {{\rm{cm}}} \right)\) là độ dài cạnh còn lại \((0 < x < 16,\,\,0 < y < 8)\). Ta có:
\({\left( {\frac{x}{2}} \right)^2} + {y^2} = {8^2} \Leftrightarrow {y^2} = \frac{1}{4}\left( {256 - {x^2}} \right) \Leftrightarrow y = \frac{1}{2}\sqrt {256 - {x^2}} \).
Diện tích của tấm giấy hình chữ nhật đó là:
\(S = xy = x \cdot \frac{1}{2}\sqrt {256 - {x^2}} = \frac{1}{2}\sqrt {{x^2}\left( {256 - {x^2}} \right)} \) (cm2).
Đặt \(f\left( x \right) = {x^2}\left( {256 - {x^2}} \right)\) với \(0 < x < 16\), có \(f'\left( x \right) = 512x - 4{x^3}\) nên \(f'\left( x \right) = 0\) khi \(x = 8\sqrt 2 \).
Vậy giá trị lớn nhất của \(S\) bằng \(\frac{1}{2}\sqrt {f\left( {8\sqrt 2 } \right)} = 64\,\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Đáp số: \(64\).
Lời giải
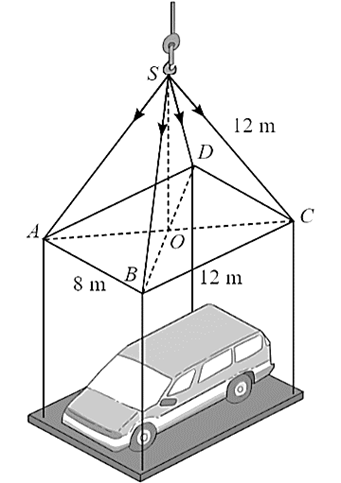
Gọi độ dài cạnh đáy của thùng chứa gạo là \(x\) (m, \(x > 0\)) và chiều cao của thùng chứa gạo là \(h\) (m, \(h > 0\)).
Thể tích của thùng là \(V = {x^2} \cdot h = 2\), suy ra \(h = \frac{2}{{{x^2}}}\) (m).
Khi đó, diện tích tôn cần sử dụng là: \[S = {x^2} + 4xh = {x^2} + 4x \cdot \frac{2}{{{x^2}}} = {x^2} + \frac{8}{x}\] (m2).
Chi phí để mua nguyên liệu là: \(T = 100{x^2} + 50 \cdot \frac{8}{x} = 100{x^2} + \frac{{400}}{x}\) (nghìn đồng).
Xét hàm số \(T\left( x \right) = 100{x^2} + \frac{{400}}{x}\) với \(x \in \left( {0; + \infty } \right)\).
Ta có: \(T'\left( x \right) = 200x - \frac{{400}}{{{x^2}}} = \frac{{200{x^3} - 400}}{{{x^2}}}\); \(T'\left( x \right) = 0\) khi \(x = \sqrt[3]{2}\).
Bảng biến thiên của hàm số \(T\left( x \right)\) trên khoảng \(\left( {0; + \infty } \right)\) như sau:
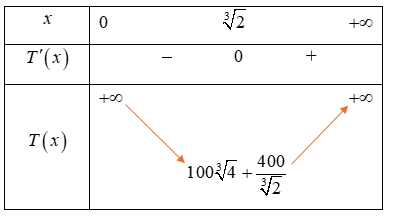
Từ bảng biến thiên ta thấy, \(T\left( x \right)\) đạt giá trị nhỏ nhất trên \(\left( {0; + \infty } \right)\) khi \(x = \sqrt[3]{2}\).
Vậy ông Hùng cần đóng thùng chứa gạo với cạnh đáy bằng \(\sqrt[3]{2} \approx 1,3\) m để chi phí mua nguyên liệu là nhỏ nhất.
Đáp số: \(1,3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo