Cho đồ thị như ở Hình 6. Em hãy cho biết:
a) Tập các đỉnh và tập các cạnh của đồ thị.
b) Các đỉnh kề với đỉnh A, D.
c) Các cạnh kề với cạnh {C, E}, {D, F}.
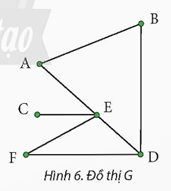
Cho đồ thị như ở Hình 6. Em hãy cho biết:
a) Tập các đỉnh và tập các cạnh của đồ thị.
b) Các đỉnh kề với đỉnh A, D.
c) Các cạnh kề với cạnh {C, E}, {D, F}.
Quảng cáo
Trả lời:
Giải bởi Vietjack
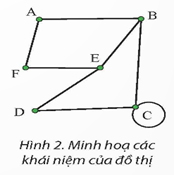
a) Tập các đỉnh của đồ thị là: {A, B, C, D, E, F}. Tập các cạnh là: {{A, B}, {A, C}, {A, D}, {B, E}, {C, E}, {D, E}, {C, F}}.
b) Các đỉnh kề với đỉnh A là: B, C, D. Các đỉnh kề với đỉnh D là: A, E.
c) Các cạnh kề với cạnh {C, E} là: {{B, E}, {D, E}, {A, C}, {C, F}}. Đối với cạnh {D, F}, không có cạnh này trong đồ thị, nhưng nếu bạn muốn biết các cạnh kề với cạnh {D, E}, đó là: {{B, E}, {C, E}, {A, D}}.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
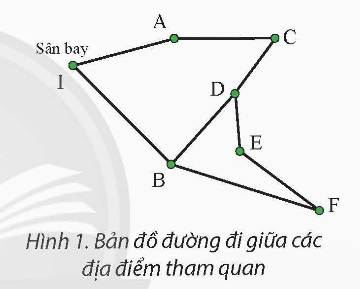
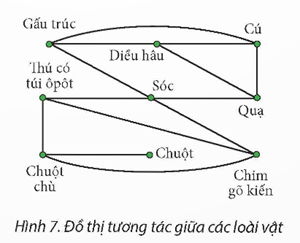
Dựa trên bản đồ đường đi giữa các địa điểm tham quan trong hình ảnh, để có một hành trình ghé thăm mỗi địa điểm một lần và quay trở lại sân bay, mỗi địa điểm cần có một số chẵn các đường nối (để tạo thành một chu trình Euler). Tuy nhiên, trong hình ảnh:
Địa điểm B và D có số lượng đường nối lẻ.
Địa điểm F và Sân bay chỉ có một đường nối.
Do đó, dựa trên nguyên tắc của đường đi Euler và không có thông tin thêm về hướng di chuyển hay khoảng cách, một hành trình như vậy không tồn tại.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
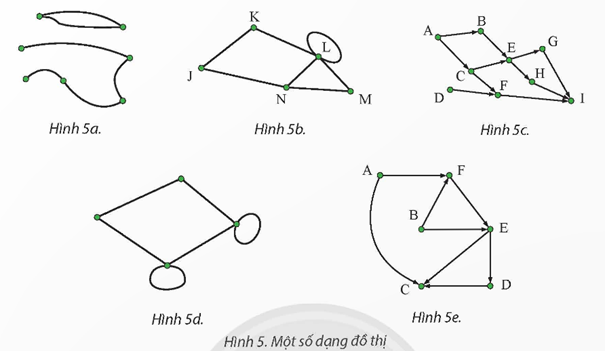
Đơn đồ thị: Là đồ thị không có vòng lặp và không có nhiều cạnh giữa cùng một cặp đỉnh. “Hình 5b” biểu diễn một đơn đồ thị.
Đồ thị vô hướng: Là đồ thị mà các cạnh không có hướng. Các đồ thị trong “Hình 5a,” “Hình 5b,” và “Hình 5c” là đồ thị vô hướng vì các cạnh của chúng không có mũi tên chỉ hướng.
Đồ thị có hướng: Là đồ thị có các cạnh được biểu diễn bằng mũi tên chỉ hướng. Trong hình ảnh này, chỉ có “Hình 5e” phù hợp với mô tả này vì nó rõ ràng thể hiện mũi tên trên các cạnh của nó.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập