Câu hỏi:
03/10/2024 2,091
Cho tam giác \(ABC\) có đường cao\(AH.\) Gọi \(D\) và \(E\) lần lượt là chân đường vuông góc kẻ từ \(H\) đến \(AB,\,\,AC.\) Chứng minh rằng \(\frac{{{S_{\Delta ADE}}}}{{{S_{\Delta ABC}}}} = {\sin ^2}B \cdot {\sin ^2}C\).
Cho tam giác \(ABC\) có đường cao\(AH.\) Gọi \(D\) và \(E\) lần lượt là chân đường vuông góc kẻ từ \(H\) đến \(AB,\,\,AC.\) Chứng minh rằng \(\frac{{{S_{\Delta ADE}}}}{{{S_{\Delta ABC}}}} = {\sin ^2}B \cdot {\sin ^2}C\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
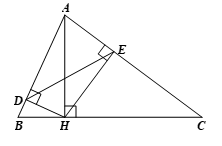
⦁ Xét \(\Delta ABD\) vuông tại \(D\) ta có: \(\cos \widehat {DAH} = \frac{{AD}}{{AH}}.\)
Xét \(\Delta ABH\) vuông tại \(H\) ta có: \(\cos \widehat {BAH} = \frac{{AH}}{{AB}}.\)
Suy ra \(\frac{{AD}}{{AH}} = \frac{{AH}}{{AB}}\) hay \(A{H^2} = AD \cdot AB\).
Chứng minh tương tự ta cũng có: \(A{H^2} = AE \cdot AC\).
Do đó \(AD \cdot AB = AE \cdot AC\) hay \(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}\).
Xét \(\Delta ADE\) và \(\Delta ACB\) có: \(\widehat {BAC}\) là góc chung và \(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}\)
Do đó (c.g.c), suy ra \(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}} = \frac{{DE}}{{CB}}\) và \(\widehat {B\,} = \widehat {E\,}\).
⦁ Xét \(\Delta ABH\) vuông tại \(H\), ta có \(AH = AB \cdot \sin B\).
Suy ra \({S_{\Delta ABC}} = \frac{1}{2}BC \cdot AH = \frac{1}{2} \cdot BC \cdot BA \cdot \sin B\).
Chứng minh tương tự, ta cũng có: \({S_{\Delta ADE}} = \frac{1}{2} \cdot ED \cdot EA \cdot \sin E\)
Khi đó, \(\frac{{{S_{\Delta ADE}}}}{{{S_{\Delta ABC}}}} = \frac{{\frac{1}{2} \cdot ED \cdot EA \cdot \sin E}}{{\frac{1}{2} \cdot BC \cdot BA \cdot \sin B}} = \frac{{DE}}{{CB}} \cdot \frac{{AE}}{{AB}} \cdot \frac{{\sin E}}{{\sin E}}\) (do \(\widehat {B\,} = \widehat {E\,})\)
Suy ra \(\frac{{{S_{\Delta ADE}}}}{{{S_{\Delta ABC}}}} = {\left( {\frac{{AE}}{{AB}}} \right)^2}\) (do \(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}} = \frac{{DE}}{{CB}})\)
Do đó \(\frac{{{S_{\Delta ADE}}}}{{{S_{\Delta ABC}}}} = {\left( {\frac{{AE}}{{AH}} \cdot \frac{{AH}}{{AB}}} \right)^2}\)
Xét \(\Delta AHE\) vuông tại \(E\) ta có: \(\frac{{AE}}{{AH}} = \cos \widehat {HAC} = \sin C\) (do \(\widehat {HAC} + \widehat {C\,} = 90^\circ )\)
Xét \(\Delta ABH\) vuông tại \(H\) ta có: \(\frac{{AH}}{{AB}} = \sin B\)
Từ đó, ta có \(\frac{{{S_{\Delta ADE}}}}{{{S_{\Delta ABC}}}} = {\left( {\frac{{AE}}{{AH}} \cdot \frac{{AH}}{{AB}}} \right)^2} = {\left( {\sin C \cdot \sin B} \right)^2} = {\sin ^2}B \cdot {\sin ^2}C.\)
Vậy \(\frac{{{S_{\Delta ADE}}}}{{{S_{\Delta ABC}}}} = {\sin ^2}B \cdot {\sin ^2}C.\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: C
![Cho tam giác \(ABC\) vuông tại \(A\) có \[BC = a,\] \[AC = b,\,\,AB = c.\] Khẳng định nào sau đây là đúng? A. \[\sin B = \frac{c}{a}\]. B. \[c = \frac{b}{{\cot B}}\]. C. \[c = b \cdot \tan C\]. D. \[b = c \cdot \cos C\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1727918783.png)
Tam giác \(ABC\) vuông tại \(A\), ta có:
⦁ \[\sin B = \frac{{AC}}{{BC}} = \frac{b}{a}\];
⦁ \(AC = BC \cdot \cos C\) hay \(b = a \cdot \cos C\);
⦁ \(AB = AC \cdot \tan C\) hay \(c = b \cdot \tan C\);
⦁ \(\cot B = \frac{{AB}}{{AC}} = \frac{c}{b}\) suy ra \(b = \frac{c}{{\cot B}}\).
Vậy phương án C là khẳng định đúng![Cho tam giác \[ABC\] vuông tại \(A\) có \(AB = 6\,\,{\rm{cm}}\) và \(\cos B = \frac{3}{5}.\) Tính độ dài các cạnh \(BC,\,\,AC\) và số đo góc \(C\) (làm tròn kết quả số đo góc đến phút). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid4-1727919496.png)
Lời giải
![Cho tam giác \[ABC\] vuông tại \(A\) có \(AB = 6\,\,{\rm{cm}}\) và \(\cos B = \frac{3}{5}.\) Tính độ dài các cạnh \(BC,\,\,AC\) và số đo góc \(C\) (làm tròn kết quả số đo góc đến phút). (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid3-1727919474.png)
1. Xét \(\Delta ABC\) vuông tại \(A,\) ta có:
⦁ \(AB = BC \cdot \cos B\) suy ra \[BC = \frac{{AB}}{{\cos B}} = \frac{6}{{\frac{3}{5}}} = 10{\rm{\;(cm)}}{\rm{.}}\]
⦁ \(B{C^2} = A{B^2} + A{C^2}\)
Suy ra \(A{C^2} = B{C^2} - A{B^2} = {10^2} - {6^2} = 64,\) nên \[AC = 8{\rm{\;cm}}{\rm{.}}\]
⦁ \(\widehat {B\,} + \widehat {C\,} = 90^\circ \) suy ra \(\sin C = \cos B = \frac{3}{5}\), từ đó ta tìm được \(\widehat {C\,} \approx 36^\circ 52'\).
2. Đặt: \(BC = x\,\,\left( {\rm{m}} \right);\) \(AC = AB + BC = 500 + x\,\,\left( {\rm{m}} \right)\).
Xét \(\Delta ACD\) vuông tại \(C,\) ta có: \[CD = AC \cdot {\rm{tan}}\widehat {CAD} = \left( {500 + x} \right) \cdot {\rm{tan}}34^\circ .\]
Xét \(\Delta BCD\) vuông tại \(C,\) ta có: \(CD = BC \cdot {\rm{tan}}\widehat {CBD} = x \cdot {\rm{tan}}38^\circ \).
Do đó, ta có: \(\;\left( {500 + x} \right) \cdot {\rm{tan}}34^\circ = x \cdot {\rm{tan}}38^\circ \)
\(500 \cdot {\rm{tan}}34^\circ + x \cdot {\rm{tan}}34^\circ = x \cdot {\rm{tan}}38^\circ \)
\(\;x \cdot {\rm{tan}}38^\circ - x \cdot {\rm{tan}}34^\circ = 500 \cdot {\rm{tan}}34^\circ \)
\(\;x \cdot \left( {{\rm{tan}}38^\circ - {\rm{tan}}34^\circ } \right) = 500 \cdot {\rm{tan}}34^\circ \)
\(\;x = \frac{{500 \cdot {\rm{tan}}34^\circ }}{{{\rm{tan}}38^\circ - {\rm{tan}}34^\circ }} \approx 3\,\,158,5\,\,({\rm{m)}}{\rm{.}}\)
Suy ra \(CD = x \cdot {\rm{tan}}38^\circ \approx 3\,\,158,5 \cdot {\rm{tan}}38^\circ \approx 2468\,\,({\rm{m}}).\)
Vậy ngọn núi cao khoảng \(2\,\,468\) mét.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo