PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
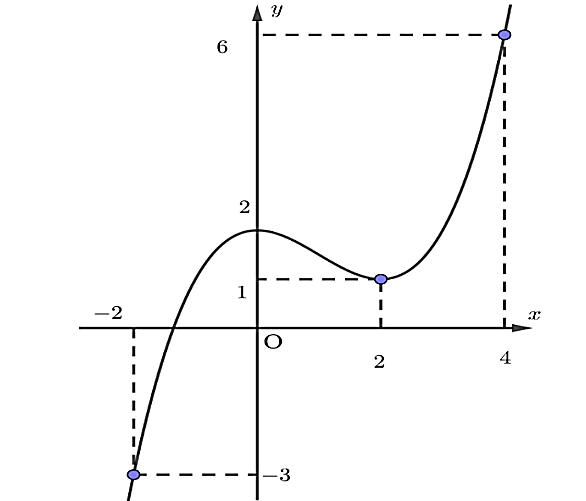
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình dưới đây.
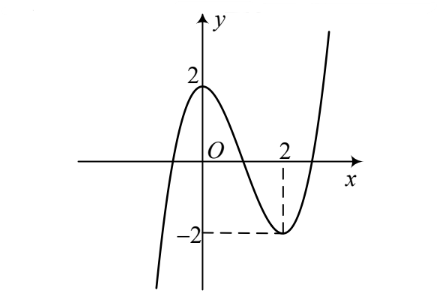
a) Hàm số đã cho đồng biến trên khoảng \(\left( {2;\, + \infty } \right)\).
b) Hàm số đã cho đạt cực đại tại \(x = 0\); đạt cực tiểu tại \(x = 2\).
c) Trên đoạn \(\left[ {0;\,2} \right]\), giá trị lớn nhất của hàm số đã cho bằng \(0\).
d) Phương trình \(3f\left( x \right) + 4 = 0\) có 3 nghiệm.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình dưới đây.

a) Hàm số đã cho đồng biến trên khoảng \(\left( {2;\, + \infty } \right)\).
b) Hàm số đã cho đạt cực đại tại \(x = 0\); đạt cực tiểu tại \(x = 2\).
c) Trên đoạn \(\left[ {0;\,2} \right]\), giá trị lớn nhất của hàm số đã cho bằng \(0\).
d) Phương trình \(3f\left( x \right) + 4 = 0\) có 3 nghiệm.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 12 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
a) Đ, b) Đ, c) S, d) Đ.
Hướng dẫn giải
Quan sát đồ thị hàm số, ta thấy:
– Hàm số đã cho đồng biến trên khoảng \(\left( {2;\, + \infty } \right)\) do trên khoảng này đồ thị của hàm số đi lên từ trái qua phải. Vậy ý a) đúng.
– Hàm số đã cho đạt cực đại tại \(x = 0\); đạt cực tiểu tại \(x = 2\). Do đó, ý b) đúng.
– Trên đoạn \(\left[ {0;\,2} \right]\), hàm số đạt giá trị lớn nhất tại \(x = 0\), \(\mathop {\max }\limits_{\left[ {0;\,2} \right]} f\left( x \right) = f\left( 0 \right) = 2\). Do đó, ý c) sai.
– Ta có \(3f\left( x \right) + 4 = 0\)\( \Leftrightarrow f\left( x \right) = - \frac{4}{3}\).
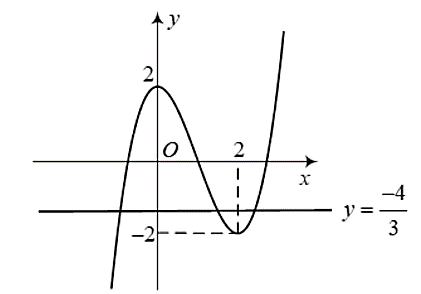
Đường thẳng \(y = - \frac{4}{3}\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm nên phương trình \(f\left( x \right) = - \frac{4}{3}\) có 3 nghiệm, tức là phương trình \(3f\left( x \right) + 4 = 0\) có 3 nghiệm.
Vậy ý d) đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta thấy \(M\left( x \right) = \frac{{0,0001{x^2} + 0,2x + 10\,000}}{x} = 0,0001x + \frac{{10\,000}}{x} + 0,2\).
Xét hàm số \(M\left( x \right) = 0,0001x + \frac{{10\,000}}{x} + 0,2\), với \(x \ge 1\).
Ta có: \(M'\left( x \right) = 0,0001 - \frac{{10\,000}}{{{x^2}}}\);
\(M'\left( x \right) = 0 \Leftrightarrow x = 10\,000\,\,\,\left( {{\rm{do}}\,\,x \ge 1} \right)\).
Bảng biến thiên của hàm số như sau:
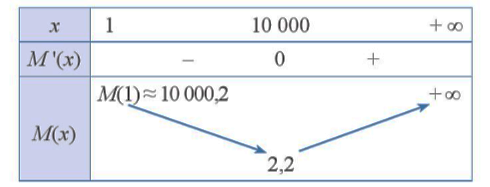
Căn cứ bảng biến thiên, ta có: \(\mathop {\min }\limits_{\left[ {1;\, + \infty } \right)} M\left( x \right) = 2,2\) tại \(x = 10\,000\).
Vậy doanh nghiệp cần sản xuất \(10\,000\) sản phẩm để chi phí trung bình là nhỏ nhất.
Đáp số: \(10\,000\).
Câu 2
Lời giải
Đáp án đúng là: A
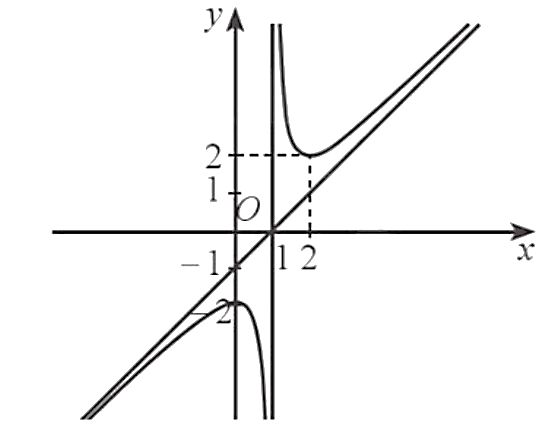
Dựa vào đồ thị hàm số, ta thấy tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng đi qua hai điểm \(\left( {1;0} \right)\) và \(\left( {0; - 1} \right)\), chính là đường thẳng \(y = x - 1\).
Do đó, đường thẳng \(y = x - 1\) là tiệm cận xiên của đồ thị hàm số đã cho.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.