Tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^2} - x + 3}}{{2x + 1}}\) là đường thẳng:

Vận tốc tức thời của chất điểm là \(v = s' =  - \pi \sin \left( {2\pi t} \right)\).

Gia tốc tức thời của chất điểm là \(a = v' =  - 2{\pi ^2}\cos \left( {2\pi t} \right)\).

Ta có: \( - 1 \le \cos \left( {2\pi t} \right) \le 1\)\( \Leftrightarrow  - 2{\pi ^2} \le  - 2{\pi ^2}\cos \left( {2\pi t} \right) \le 2{\pi ^2}\) với mọi \(t\).

Tức là \( - 2{\pi ^2} \le a \le 2{\pi ^2}\). Vậy \({a_{\max }} = 2{\pi ^2} \approx 19,7\) với \(\cos \left( {2\pi t} \right) =  - 1 \Rightarrow t = \frac{1}{2} + k,\,k \in \mathbb{Z}\).

Vậy gia tốc lớn nhất của chất điểm bằng khoảng \(19,7\) m/s2.

Đáp số: \(19,7\).

Từ giả thiết, ta suy ra được:

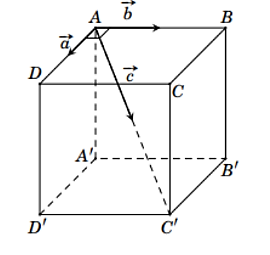
\(\overrightarrow a  \bot \overrightarrow b ;\,\,\cos \left( {\overrightarrow a ,\,\overrightarrow c } \right) = \cos \widehat {DAC'} = \frac{1}{{\sqrt 3 }}\); \(\cos \left( {\overrightarrow b ,\overrightarrow c } \right) = \cos \widehat {BAC'} = \frac{1}{{\sqrt 3 }}\).

Giả sử lực tổng hợp là \(\overrightarrow m \), tức là \(\overrightarrow m  = \overrightarrow a  + \overrightarrow b  + \overrightarrow c \).

Khi đó, \({\overrightarrow m ^2} = {\left( {\overrightarrow a  + \overrightarrow b  + \overrightarrow c } \right)^2}\)\( = {\overrightarrow a ^2} + {\overrightarrow b ^2} + {\overrightarrow c ^2} + 2\overrightarrow a  \cdot \overrightarrow b  + 2\overrightarrow b  \cdot \overrightarrow c  + 2\overrightarrow c  \cdot \overrightarrow a \)

\( = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} + {\left| {\overrightarrow c } \right|^2} + 0 + 2\left| {\overrightarrow b } \right| \cdot \left| {\overrightarrow c } \right| \cdot \cos \left( {\overrightarrow b ,\overrightarrow c } \right) + 2\left| {\overrightarrow c } \right| \cdot \left| {\overrightarrow a } \right| \cdot \cos \left( {\overrightarrow c ,\overrightarrow a } \right)\)

\( = {10^2} + {10^2} + {20^2} + 2 \cdot 10 \cdot 20 \cdot \frac{1}{{\sqrt 3 }} + 2 \cdot 10 \cdot 20 \cdot \frac{1}{{\sqrt 3 }}\)

\( = 600 + \frac{{800}}{{\sqrt 3 }}\).

Suy ra \({\left| {\overrightarrow m } \right|^2} = {\overrightarrow m ^2} = 600 + \frac{{800}}{{\sqrt 3 }}\). Do đó, \(\left| {\overrightarrow m } \right| = \sqrt {600 + \frac{{800}}{{\sqrt 3 }}}  \approx 32,6\).

Vậy độ lớn hợp lực của các lực \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \) bằng khoảng \(32,6\) N.

Đáp số: \(32,6\).