Cho hàm số \(y = \frac{{x - 3}}{{x + 1}}\).
a) Hàm số đã cho đồng biến trên \[\mathbb{R}\backslash \left\{ { - 1} \right\}\].
b) Hàm số đã cho đạt cực đại tại \(x = 4\).
c) Đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng \(x = - 1\), tiệm cận ngang là đường thẳng \(y = 1\).
d) Có \(2\,023\) giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 2\,024;2\,024} \right]\) để đường thẳng \(y = x + 2m\) cắt đồ thị hàm số đã cho tại hai điểm nằm về hai phía của trục tung.
Cho hàm số \(y = \frac{{x - 3}}{{x + 1}}\).
a) Hàm số đã cho đồng biến trên \[\mathbb{R}\backslash \left\{ { - 1} \right\}\].
b) Hàm số đã cho đạt cực đại tại \(x = 4\).
c) Đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng \(x = - 1\), tiệm cận ngang là đường thẳng \(y = 1\).
d) Có \(2\,023\) giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 2\,024;2\,024} \right]\) để đường thẳng \(y = x + 2m\) cắt đồ thị hàm số đã cho tại hai điểm nằm về hai phía của trục tung.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 12 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
a) S, b) S, c) Đ, d) Đ.
Hướng dẫn giải
Xét hàm số \(y = \frac{{x - 3}}{{x + 1}}\).
– Tập xác định của hàm số là \(\mathbb{R}\backslash \left\{ { - 1} \right\}\).
– Ta có \(y' = \frac{4}{{{{\left( {x + 1} \right)}^2}}}\); \(y' > 0\) với mọi \(x \ne - 1\).
– Hàm số đã cho đồng biến trên từng khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\). Do đó, ý a) sai.
– Hàm số đã cho không có cực trị. Do đó, ý b) sai.
– Tiệm cận:
+) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{x - 3}}{{x + 1}} = 1;\,\mathop {\lim }\limits_{x \to - \infty } \frac{{x - 3}}{{x + 1}} = 1\). Do đó, tiệm cận ngang của đồ thị hàm số đã cho là đường thẳng \(y = 1\).
+) \(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{x - 3}}{{x + 1}} = - \infty ;\,\mathop {\lim }\limits_{x \to - {1^ - }} \frac{{x - 3}}{{x + 1}} = + \infty \). Do đó, tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng \(x = - 1\).
Vậy ý c) đúng.
– Phương trình hoành độ giao điểm của đường thẳng \(y = x + 2m\,\,\left( d \right)\) và đồ thị hàm số \(y = \frac{{x - 3}}{{x + 1}}\,\,\left( C \right)\) là: \(\frac{{x - 3}}{{x + 1}} = x + 2m\)\( \Leftrightarrow \left( {x + 1} \right)\left( {x + 2m} \right) = x - 3\)\( \Leftrightarrow {x^2} + 2mx + 2m + 3 = 0\).
Xét hàm số \(g\left( x \right) = {x^2} + 2mx + 2m + 3\).
\(\left( d \right)\) cắt \(\left( C \right)\) tại hai điểm nằm về hai phía của trục tung khi phương trình \(g\left( x \right) = 0\) có hai nghiệm \({x_1};\,{x_2}\) khác \( - 1\) và \({x_1}{x_2} < 0\). Điều này xảy ra khi và chỉ khi
\[\left\{ {\begin{array}{*{20}{c}}\begin{array}{l}{\Delta _g} > 0\\g\left( { - 1} \right) \ne 0\end{array}\\{\frac{c}{a} < 0\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 2m - 3 > 0\\1 - 2m + 2m + 3 \ne 0\\2m + 3 < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m < - 1\\m > 3\end{array} \right.\\m < - \frac{3}{2}\end{array} \right.\)\( \Leftrightarrow m < - \frac{3}{2}\).
Vì \(m \in \mathbb{Z},\,\,m \in \left[ { - 2\,024;\,2\,024} \right]\) nên \(m \in \left\{ { - 2\,024;\, - 2\,023;\,...; - 2} \right\}\).
Vậy có \(2\,023\) giá trị của \(m\) thỏa mãn.
Do đó, ý d) đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
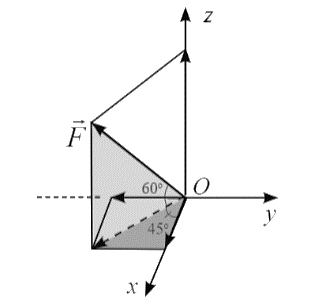
Đặt \(\overrightarrow F = \left( {x;y;z} \right)\), ta có:
\(x = 200 \cdot \cos 60^\circ \cdot \cos 45^\circ = 50\sqrt 2 \);
\(y = - 200 \cdot \cos 60^\circ \cdot \cos 45^\circ = - 50\sqrt 2 \);
\(z = 200 \cdot \sin 60^\circ = 100\sqrt 3 \).
Do đó, \(\overrightarrow F = \left( {50\sqrt 2 ; - 50\sqrt 2 ;100\sqrt 3 } \right)\).
Suy ra \(a = 50,b = 50,c = 100\). Vậy \(K = a - 2b + c = 50 - 2 \cdot 50 + 100 = 50\).
Đáp số: \(50\).
Câu 2
Lời giải
Đáp án đúng là: A
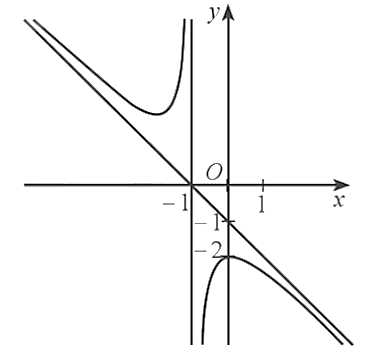
Dựa vào đồ thị hàm số đã cho ta có:
+ Đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = - 1\) nên ta loại phương án C.
+ Đồ thị hàm số có tiệm cận xiên là đường thẳng đi xuống từ trái qua phải nên \(a,\,m\) trái dấu. Vậy phương án đúng là A.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.