Công thức \(h = 0,4 \cdot \sqrt[3]{x}\) biểu diễn mối liên hệ giữa cân nặng \(x\) (kg) và chiều cao \(h\) (m) của một con hươu cao cổ ở tuổi trưởng thành (Nguồn: Math for Real Life: Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby, năm 2017). Một con hươu cao cổ có chiều cao là \(2,68\) m thì nặng bao nhiêu kilôgam (làm tròn kết quả đến hàng đơn vị)?
A. 300 kg.
B. 301 kg.
C. 302 kg.
D. 303 kg.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
Với \(h = 2,68\) (m), ta có:
\(2,68 = 0,4 \cdot \sqrt[3]{x}\)
\(\sqrt[3]{x} = 6,7\)
\(x \approx 301\).
Vậy con hươu cao cổ có chiều cao là \(2,68\) m thì nặng khoảng \(301\) kg.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
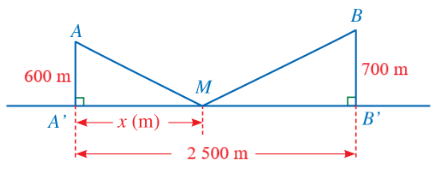
A. \[MB = \sqrt {360\,\,000 + {x^2}} \].
B. \[MA + MB = \left( {360\,\,000 + {x^2}} \right) + \left[ {490\,\,000 + {{\left( {2\,\,500 - x} \right)}^2}} \right]\].
C. Khi \(x = 1\,\,200\) thì tổng khoảng cách \[MA + MB\] khoảng 2 818 m.
D. Cả A, B, C đều đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: C
⦁ Áp dụng định lí Pythagore cho \(\Delta AA'M\) vuông tại \(A'\) ta có:
\(M{A^2} = A{A'^2} + A'{M^2} = {600^2} + {x^2} = 360\,\,000 + {x^2}\)
Suy ra \[MA = \sqrt {360\,\,000 + {x^2}} \] (m).
Ta có \(A'B' = A'M + B'M,\) suy ra \(B'M = A'B' - A'M = 2\,\,500 - x{\rm{\;(m)}}{\rm{.}}\)
Áp dụng định lí Pythagore cho \(\Delta BB'M\) vuông tại \(B'\) ta có:
\[M{B^2} = B{B'^2} + {\rm{ }}B'{M^2} = {700^2} + {\left( {2{\rm{ }}500--x} \right)^2} = 490{\rm{ }}000 + {\left( {2{\rm{ }}500--x} \right)^2}\]
Suy ra \[MB = \sqrt {490{\rm{ }}000 + {{\left( {2{\rm{ }}500--x} \right)}^2}} \] (m).
Khi đó, tổng khoảng cách \[MA + MB\] theo \[x\] là:
\[MA + MB = \sqrt {360\,\,000 + {x^2}} + \sqrt {490\,\,000 + {{\left( {2\,\,500 - x} \right)}^2}} \] (m).
Khi \[x = 1{\rm{ }}200,\] ta có tổng khoảng cách \[MA + MB\] là:
⦁ \[MA + MB = \sqrt {360\,\,000 + 1\,\,{{200}^2}} + \sqrt {490\,\,000 + {{\left( {2\,\,500 - 1\,\,200} \right)}^2}} \]
\[ = \sqrt {1\,\,800\,\,000} + \sqrt {2\,\,180\,\,000} \]
\[ \approx 2\,\,818{\rm{\;(m)}}{\rm{.}}\]
Vậy tổng khoảng cách \[MA + MB\] khoảng 2 818 m khi \(x = 1\,\,200\).
Câu 2
A. \(\sqrt {x + 2} \).
B. \(\sqrt 2 \).
C. \(\sqrt {\frac{1}{x}} \).
D. \(1 - 2\sqrt x \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
Biểu thức \(1 - 2\sqrt x \) không là căn thức bậc hai.
Câu 3
A. 6.
B. \(\sqrt[3]{{\frac{1}{x}}}\).
C. \(1 + \sqrt[3]{x}.\)
D. \(\sqrt[3]{6}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{{42\sqrt 5 }}{5}\) m/s.
B. \(18,7\) m/s.
C. \(18,8\) m/s.
D. \(18,78\) m/s.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(x > 0.\)
B. \(x < 0.\)
</>
C. \(x \ge 0.\)
D. \(x \in \mathbb{R}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(x \ne 1.\)
B. \(x > 1.\)
C. \(x < 1.\)
</>
D. \(x \in \mathbb{R}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập