II. Thông hiểu
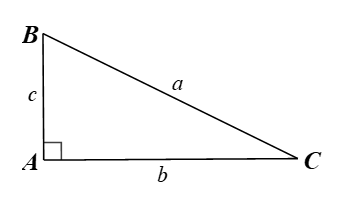
Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 20{\rm{\;cm}},\,\,\widehat {C\,} = 60^\circ .\] Độ dài cạnh \[BC\] bằng
A. \[40\] (cm).
B. \[40\sqrt 3 \] (cm).
C. \[20\sqrt 3 \] (cm).
D. \[20\] (cm).
Quảng cáo
Trả lời:
Đáp án đúng là: A
![Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 20{\rm{\;cm}},\,\,\widehat {C\,} = 60^\circ .\] Độ dài cạnh \[BC\] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1729481262.png)
Vì tam giác \[ABC\] vuông tại \[A\] nên \[AC = BC.\cos C.\]
Suy ra \[BC = \frac{{AC}}{{\cos C}} = \frac{{20}}{{\cos 60^\circ }} = 40\] (cm).
Vậy ta chọn phương án A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[2\,\,716\] mét.
B. \[2\,\,301\] mét.
C. \[977\] mét.
D. \[6\,\,398\] mét.
Lời giải
Đáp án đúng là: D
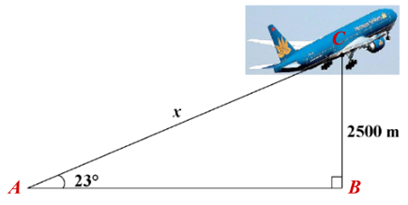
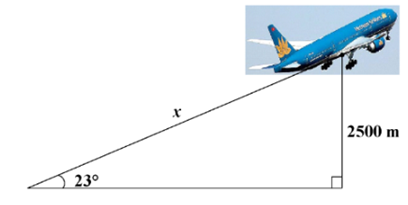
Theo đề, ta có \[\widehat {BAC} = 23^\circ \] và \[BC = 2\,\,500\] (m).
Vì tam giác \[ABC\] vuông tại \[B\] nên \[\sin \widehat {BAC} = \frac{{BC}}{{AC}}.\]
Suy ra \[AC = \frac{{BC}}{{\sin \widehat {BAC}}}\] hay \[x = \frac{{2\,\,500}}{{\sin 23^\circ }} \approx 6\,\,398\] (m).
Do đó muốn đạt độ cao \[2500\] m thì máy bay phải bay một đoạn đường \[x\] dài \[6\,\,398\] mét.
Vậy ta chọn phương án D.
Câu 2
A. \[30^\circ.\]
B. \[40^\circ.\]
C. \[50^\circ.\]
D. \[60^\circ.\]
Lời giải
Đáp án đúng là: A
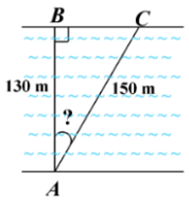
Ta có dòng nước đã đẩy con đò đi lệch một góc \[\widehat {BAC}\] so với dự định ban đầu.
Theo đề, ta có \[BA = 130\] (m) và \[AC = 150\] (m).
Vì tam giác \[ABC\] vuông tại \[B\] nên \[\cos \widehat {BAC} = \frac{{BA}}{{AC}} = \frac{{130}}{{150}} = \frac{{13}}{{15}}.\]
Suy ra \[\widehat {BAC} \approx 30^\circ .\]
Do đó dòng nước đã đẩy con đò đi lệch một góc \[30^\circ \] so với phương dự định ban đầu.
Vậy ta chọn phương án A.
Câu 3
A. \[BC = \sqrt {74} {\rm{\;cm}};\,\,\widehat C \approx 35^\circ 32'.\]
B. \[BC = \sqrt {74} {\rm{\;cm}};\,\,\widehat C \approx 54^\circ 28'.\]
C. \[BC = 2\sqrt 6 {\rm{\;cm}};\,\,\widehat {C\,} \approx 35^\circ 32'.\]
D. \[BC = 2\sqrt 6 {\rm{\;cm}};\,\,\widehat C \approx 54^\circ 28'.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. sin.
B. côsin.
C. tang.
D. côtang.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
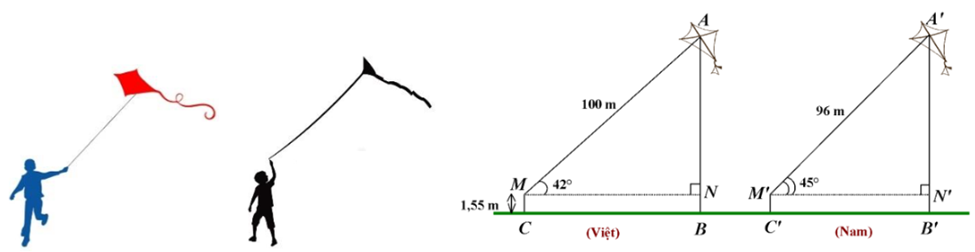
A. So với mặt đất thì diều của bạn Việt lên cao hơn diều của bạn Nam và cao hơn \[0,25\] m.
B. So với mặt đất thì diều của bạn Nam lên cao hơn diều của bạn Việt và cao hơn \[0,97\] m.
C. So với mặt đất thì diều của bạn Nam lên cao hơn diều của bạn Việt và cao hơn \[1,03\] m.
D. So với mặt đất thì diều của hai bạn Việt và Nam lên cao bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[5\] (đvdt).
B. \[4\] (đvdt).
C. \[3\] (đvdt).
D. \[2\] (đvdt).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[c = a.\cot B.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Một khúc sông rộng khoảng \[250\] m. Một con đò chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng \[320\] m mới sang được bờ bên kia. Giả sử dòng nước đã đẩy con đò đi lệch một góc \[\ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1729481212.png)