Cho tam giác \[ABC\] vuông tại \[A\] có \[AB = 5{\rm{\;cm}},\,\,\cos B = \frac{5}{8}.\] Kết quả nào sau đây là đúng?
A. \[BC = \sqrt {39} \] cm; \[AC = 8\] cm.
B. \[BC = 8\] cm; \[AC = \sqrt {39} \] cm.
C. \[BC = 16\] cm; \[AC = \sqrt {39} \] cm.
D. \[BC = 4\] cm; \[AC = \frac{{\sqrt {39} }}{2}\] cm.
Quảng cáo
Trả lời:
Đáp án đúng là: B

Xét tam giác \[ABC\] vuông tại \[A\], có:
⦁ \[\cos B = \frac{{AB}}{{BC}}.\] Suy ra \[BC = \frac{{AB}}{{\cos B}} = \frac{5}{{\frac{5}{8}}} = 8\] (cm);
⦁ \[B{C^2} = A{B^2} + A{C^2}\] (theo định lí Pythagore)
Suy ra \[A{C^2} = B{C^2} - A{B^2} = {8^2} - {5^2} = 39.\] Do đó \[AC = \sqrt {39} \] (cm).
Vậy ta chọn phương án B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
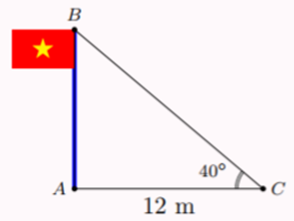
A. \[10,069\] m.
B. \[10,07\] m.
C. \[10,06\] m.
D. \[10,7\] m.
Lời giải
Đáp án đúng là: B
Vì tam giác \[ABC\] vuông tại \[A\] nên \[AB = AC.\tan C = 12.\tan 40^\circ \approx 10,07\] (m).
Do đó chiều cao \[AB\] của cột cờ khoảng \[10,07\] m.
Vậy ta chọn phương án B.
Câu 2
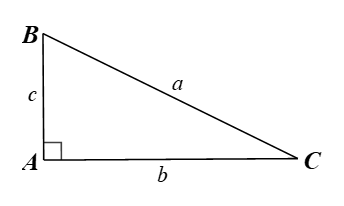
A. \[c = a\sin B.\]
Lời giải
Đáp án đúng là: C
Vì tam giác \[ABC\] vuông tại \[A\] nên:
⦁ \[b = a\sin B = a\cos C = c\tan B = c\cot C\,;\]
⦁ \[c = a\sin C = a\cos B = c\tan B = c\cot C.\]
Vậy ta chọn phương án C.
Câu 3
A. \[A\] m.
B. \[5\] m.
C. \[6\] m.
D. \[7\] m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[\frac{9}{{14}}.\]
B. \[\frac{{18}}{7}.\]
C. \[\frac{{63}}{2}.\]
D. \[\frac{{14}}{9}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[1{\rm{\;\;}}783\] m.
B. \[1{\rm{\;\;}}841\] m.
C. \[1{\rm{\;\;}}652\] m.
D. \[1{\rm{\;\;}}906\] m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[\frac{{\sqrt 2 }}{2}.\]
B. \[\frac{1}{2}.\]
C. \[\frac{{\sqrt 3 }}{2}.\]
D. \[\sqrt 3 .\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[1,6\] mét.
B. \[1,9\] mét.
C. \[2,1\] mét.
D. \[3,0\] mét.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.