Câu hỏi:
22/10/2024 235Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh \(a,SA \bot (ABC)\), góc giữa SC và mặt phẳng \((ABC)\) bằng . Tính khoảng cách giữa hai đường thẳng SB và AC.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp giải
Bước 1: Do \(SA \bot (ABC)\) nên góc giữa SC và mặt phẳng \((ABC)\) là góc \(\widehat {SCA}\). Tìm SA
Bước 2: Lấy điểm \(D\) sao cho ACBD là hình bình hành. Khi đó \(d(SB,AC) = d(AC,(SBD)) = d(A,(SBD))\).
Ta có \(\Delta ABD\) đều cạnh \(a\). Gọi \(M\) là trung điểm \(BD \to AM\)
Bước 3: Trong \(\Delta SAM\) kẻ \(AH \bot SM\) với \(H \in SM\). Suy ra \(AH \bot (SAM) \Rightarrow d(A,(SBD)) = AH\)
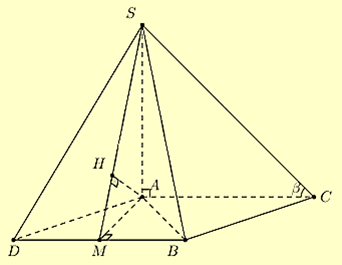
Do \(SA \bot (ABC)\) nên góc giữa SC và mặt phẳng \((ABC)\) là góc \(\widehat {SCA}\). Suy ra \(\widehat {SCA} = {30^^\circ }\) Trong tam giác SCA vuông tại \(A\):
Có \(\tan \widehat {SCA} = \frac{{SA}}{{AC}} \leftrightarrow SA = AC.\tan \widehat {SCA} = a.\tan {30^^\circ } = \frac{{a\sqrt 3 }}{3}\)
Lấy điểm \(D\) sao cho ACBD là hình bình hành.
Khi đó \(d(SB,AC) = d(AC,(SBD)) = d(A,(SBD))\).
Ta có \(AB = BD = AD \Rightarrow \Delta ABD\) đều cạnh \(a\).
Gọi \(M\) là trung điểm BD. Suy ra \(AM \bot BD\) và \(AM = \frac{{a\sqrt 3 }}{2}\).
Trong \(\Delta SAM\) kẻ \(AH \bot SM\) với \(H \in SM\).
Do \(\left. {\begin{array}{*{20}{l}}{BD \bot AM}\\{BD \bot SA}\end{array}} \right\} \Rightarrow BD \bot (SAM) \Rightarrow BD \bot AH\).
Suy ra \(AH \bot (SAM) \Rightarrow d(A,(SBD)) = AH\).
Trong \(\Delta SAM\) vuông tại \(A\) ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{M^2}}} + \frac{1}{{S{A^2}}} \Leftrightarrow \frac{1}{{A{H^2}}} = \frac{4}{{3{a^2}}} + \frac{9}{{3{a^2}}}\)
\( \Leftrightarrow \frac{1}{{A{H^2}}} = \frac{{13}}{{3{a^2}}} \Leftrightarrow AH = \frac{{a\sqrt 3 }}{{\sqrt {13} }}\)
Vậy\(d(SB,AC) = \frac{{a\sqrt 3 }}{{\sqrt {13} }} = \frac{{a\sqrt {39} }}{{13}}\).
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: “28”
Phương pháp giải
Vì S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập A
Lời giải
Vì S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập A nên ta tính số phần tử thuộc tập Snhư sau:
+ Số các số thuộc S có 3 chữ số là \(A_5^3\).
+ Số các số thuộc S có 4 chữ số là \(A_5^4\).
+ Số các số thuộc S có 5 chữ số là \(A_5^5\).
Suy ra số phần tử của tập S là \(A_5^3 + A_5^4 + A_5^5 = 300.\)
Số phần tử của không gian mẫu là \({n_\Omega } = C_{300}^1 = 300\)
Gọi X là biến cố “Số được chọn có tổng các chữ số bằng 10”. Các tập con của A có tổng số phần tử bằng 10 là A1 = {1;2;3;4}, A2 = {2;3;5}, A3 = {1;4;5}.
+ Từ A1 lập được các số thuộc S là 4!.
+ Từ A2 lập được các số thuộc S là 3!.
+ Từ A3 lập được các số thuộc S là 3!.
Suy ra số phần tử của biến cố X là nX = 4! + 3! + 3! = 36.
Vậy xác suất cần tính \(P(X) = \frac{{{n_X}}}{{{n_\Omega }}} = \frac{{36}}{{300}} = \frac{3}{{25}}.\)
Lời giải
Phương pháp giải
Dạng vô định ∞ - ∞
Lời giải
Ta có \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{x^3} - 3x + 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{{(x - 1)}^2}(x + 2)}} = L,\) với \(L \in \mathbb{R}\)(*)
Khi đó \(\sqrt {a + 1} - b - 2 = 0 \Leftrightarrow \sqrt {a + 1} = b + 2 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b \ge - 2}\\{a + 1 = {b^2} + 4b + 4}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b \ge - 2}\\{a = {b^2} + 4b + 3}\end{array}} \right.\)
Thay \(a = {b^2} + 4b + 3\) vào (*):
\(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{x^3} - 3x + 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} - bx - 2}}{{{{(x - 1)}^2}(x + 2)}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {{b^2} + 4b + 3} \right){x^2} + 1 - {{(bx + 2)}^2}}}{{{{(x - 1)}^2}(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{(4b + 3){x^2} - 4bx - 3}}{{{{(x - 1)}^2}(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{(4b + 3)x + 3}}{{(x - 1)(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}} = L,\,\,L \in \mathbb{R}\)
Khi đó: \((4b + 3) + 3 = 0 \Leftrightarrow b = - \frac{3}{2} \Rightarrow a = - \frac{3}{4}.\)
Vậy \({a^2} + {b^2} = \frac{{45}}{{16}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 29)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)