Câu hỏi:
22/10/2024 267Cho lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy ABCD là hình thoi,. Góc giữa đường thẳng \({\rm{AC'}}\) và mặt phẳng \(\left( {{\rm{ADD'A'}}} \right)\) là . M là trung điểm \({\rm{A'D'}},\) N là trung điểm \({\rm{BB'}}\). Tính khoảng cách từ \({\rm{N}}\) đến mặt phẳng (\({\rm{C'MA}}\))
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp giải
Sử dụng phương pháp đổi điểm để tính khoảng cách
Lời giải
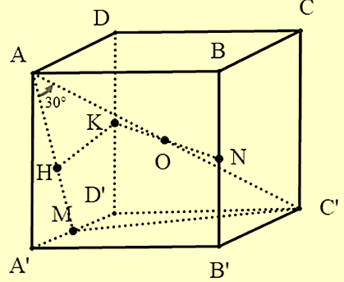
ΔA′D′C′ đều ⇒ C′M ⊥ A′D′
⇒ C′M ⊥ (AA′D′D)
\[ \Rightarrow \left( {\widehat {AC\prime ;\left( {ADD\prime A\prime } \right)}} \right) = \widehat {C\prime AM} = {30^ \circ }\]
Gọi O là trung điểm của AC′
K là trung điểm của DD′
⇒ K và N đối xứng nhau qua O
⇒ d[N,(C′MA)] = d[K,(C′MA)]
Do (C′MA) ⊥ (AA′D′D) theo giao tuyến AM nên kẻ KH ⊥ AM, ta có: KH ⊥ (C′MA)
⇒ d[K,(C′MA)] = KH
Ta có: \(C'M = a\sqrt 3 .\frac{{\sqrt 3 }}{2} = \frac{{3a}}{2}\)
Xét ΔAMC′:
Xét ΔA′AM: \(A'A = \sqrt {A{M^2} - A'{M^2}} = \sqrt {{{\left( {\frac{{3a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}} = a\sqrt 6 \)
Ta có: SAA′D′D = AA′.A′D′ = \(a\sqrt 6 .a\sqrt 3 = 3{a^2}\sqrt 2 \)
\({S_{AA'M}} = \frac{1}{2}a\sqrt 6 .\frac{{a\sqrt 3 }}{2} = \frac{{3{a^2}\sqrt 2 }}{4}\)
\({S_{MD'K}} = \frac{1}{2}.\frac{{a\sqrt 3 }}{2}.\frac{{a\sqrt 6 }}{2} = \frac{{3{a^2}\sqrt 2 }}{8}\)
\({S_{ADK}} = \frac{1}{2}.\frac{{a\sqrt 6 }}{2}.a\sqrt 3 = \frac{{3{a^2}\sqrt 2 }}{4}\)
\({S_{\Delta AMK}} = {S_{AA'D'D}} - \left( {{S_{\Delta A'AM}} + {S_{\Delta MD'K}} + {S_{\Delta ADK}}} \right)\)
\( = 3{a^2}\sqrt 2 - \left( {\frac{{3{a^2}\sqrt 2 }}{4} + \frac{{3{a^2}\sqrt 2 }}{8} + \frac{{3{a^2}\sqrt 2 }}{4}} \right) = \frac{{9{a^2}\sqrt 2 }}{8}\)
Mặt khác: \[{S_{\Delta AMK}} = \frac{1}{2}AM.KH\]
\( \Rightarrow \frac{{9{a^2}\sqrt 2 }}{8} = \frac{1}{2}.\frac{{3a\sqrt 3 }}{2}.KH\)
\( \Rightarrow KH = \frac{{a\sqrt 6 }}{2}\). Chọn C
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: “28”
Phương pháp giải
Vì S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập A
Lời giải
Vì S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập A nên ta tính số phần tử thuộc tập Snhư sau:
+ Số các số thuộc S có 3 chữ số là \(A_5^3\).
+ Số các số thuộc S có 4 chữ số là \(A_5^4\).
+ Số các số thuộc S có 5 chữ số là \(A_5^5\).
Suy ra số phần tử của tập S là \(A_5^3 + A_5^4 + A_5^5 = 300.\)
Số phần tử của không gian mẫu là \({n_\Omega } = C_{300}^1 = 300\)
Gọi X là biến cố “Số được chọn có tổng các chữ số bằng 10”. Các tập con của A có tổng số phần tử bằng 10 là A1 = {1;2;3;4}, A2 = {2;3;5}, A3 = {1;4;5}.
+ Từ A1 lập được các số thuộc S là 4!.
+ Từ A2 lập được các số thuộc S là 3!.
+ Từ A3 lập được các số thuộc S là 3!.
Suy ra số phần tử của biến cố X là nX = 4! + 3! + 3! = 36.
Vậy xác suất cần tính \(P(X) = \frac{{{n_X}}}{{{n_\Omega }}} = \frac{{36}}{{300}} = \frac{3}{{25}}.\)
Lời giải
Phương pháp giải
Dạng vô định ∞ - ∞
Lời giải
Ta có \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{x^3} - 3x + 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{{(x - 1)}^2}(x + 2)}} = L,\) với \(L \in \mathbb{R}\)(*)
Khi đó \(\sqrt {a + 1} - b - 2 = 0 \Leftrightarrow \sqrt {a + 1} = b + 2 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b \ge - 2}\\{a + 1 = {b^2} + 4b + 4}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b \ge - 2}\\{a = {b^2} + 4b + 3}\end{array}} \right.\)
Thay \(a = {b^2} + 4b + 3\) vào (*):
\(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{x^3} - 3x + 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} - bx - 2}}{{{{(x - 1)}^2}(x + 2)}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {{b^2} + 4b + 3} \right){x^2} + 1 - {{(bx + 2)}^2}}}{{{{(x - 1)}^2}(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{(4b + 3){x^2} - 4bx - 3}}{{{{(x - 1)}^2}(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{(4b + 3)x + 3}}{{(x - 1)(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}} = L,\,\,L \in \mathbb{R}\)
Khi đó: \((4b + 3) + 3 = 0 \Leftrightarrow b = - \frac{3}{2} \Rightarrow a = - \frac{3}{4}.\)
Vậy \({a^2} + {b^2} = \frac{{45}}{{16}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 29)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)