Câu hỏi:
23/10/2024 138
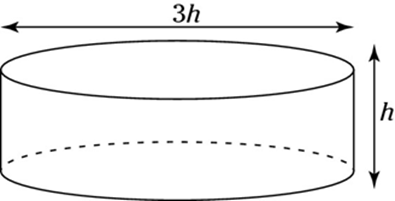
Hình dưới đây cho thấy một bể hình trụ có đường kính gấp 3 lần chiều cao của nó. Bể chứa khoảng 231,5 mét khối chất lỏng. Chiều cao của bể gần với số nào sau đây?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp giải
Sử dụng công thức tính thể tích V = π.r2.h rồi rút ra chiều cao h
Lời giải
Thể tích của bể là: \(V = \pi .{r^2}.h = \pi .{\left( {\frac{{3h}}{2}} \right)^2}.h = \frac{{9\pi }}{4}.{h^3} = 231,5\)
⇒ h ≈ 3,2m. Chọn B
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp giải
Lời giải
Ta sử dụng phương pháp trải đa diện:
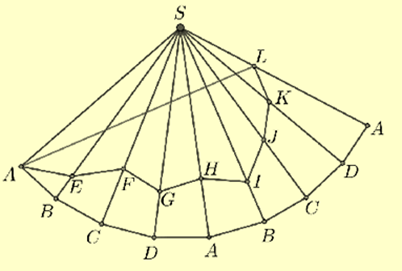
Cắt hình chóp theo cạnh bên SA rồi trải ra mặt phẳng hai lần như hình vẽ trên. Từ đó suy ra chiều dài dây đèn led ngắn nhất là bằng AL + LS.
Từ giả thiết về hình chóp đều S.ABCD ta có \[\widehat {ASL} = {120^o}\].
Ta có \[A{L^2} = S{A^2} + S{L^2} - 2SA.SL.\cos \widehat {ASL}\] \( = {200^2} + {40^2} - 2.200.40.\cos {120^^\circ } = 49600.\)
Nên \(AL = \sqrt {49600} = 40\sqrt {31} .\)
Vậy, chiều dài dây đèn led cần ít nhất là \(40\sqrt {31} + 40\) mét.
Chọn C
Lời giải
Phương pháp giải
Lời giải
Theo bài cho, tổng số viên bi có trong hộp là: n + 8 (n ∈ N*).
Lấy ngẫu nhiên 3 viên bi từ hộp. Số kết quả có thể xảy ra là: \(n(\Omega ) = C_{n + 8}^3\).
Gọi \(A\) là biến cố: "3 viên bi lấy được có đủ ba màu". Số kết quả thuận lợi cho \(A\) là:
\(n(A) = C_5^1.C_3^1.C_n^1 = 15n{\rm{. }}\)
\( \Rightarrow \) Xác suất để trong 3 viên bi lấy được có đủ ba màu là:
\(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{15n}}{{C_{n + 8}^3}} = \frac{{90n}}{{(n + 6)(n + 7)(n + 8)}}\)
Theo bài, ta có: \(P(A) = \frac{{45}}{{182}}\) nên ta được phương trình:
\(\frac{{90n}}{{(n + 6)(n + 7)(n + 8)}} = \frac{{45}}{{182}} \Leftrightarrow 364n = (n + 6)(n + 7)(n + 8)\)
\( \Leftrightarrow {n^3} + 21{n^2} - 218n + 336 = 0.\)
Giải phương trình trên với điều kiện \(n\) là số nguyên dương, ta được \(n = 6\).
Do đó, trong hộp có tất cả 14 viên bi và \(n(\Omega ) = C_{14}^3\).
Gọi \(B\) là biến cố: "3 viên bi lấy được có nhiều nhất hai viên bi đỏ". Suy ra, \(\bar B\) là biến cố: "3 viên bi lấy được đều là bi đỏ". Số kết quả thuận lợi cho \(\bar B\) là: \(n(\bar B) = C_5^3\).
Khi đó, xác suất \(P\) để trong 3 viên bi lấy được có nhiều nhất 2 viên bi đỏ là:
\(P = P(B) = 1 - P(\bar B) = 1 - \frac{{n(\bar B)}}{{n(\Omega )}} = 1 - \frac{{C_5^3}}{{C_{14}^3}} = \frac{{177}}{{182}}\).
Chọn B
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 29)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)