Câu hỏi:

23/10/2024 298

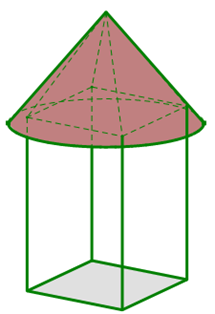
Một công ty du lịch đầu tư xây dựng 24 nhà chòi trong khu du lịch sinh thái. Mô hình thiết kế như hình vẽ, mái nhà có hình dạng là mặt xung quanh của hình nón với bán kính đáy là 3m và chiều cao của mái nhà là 4m. Chi phí làm mái là 2 triệu đồng/m2, chi phí làm hệ thống cột, khung nhà và nền nhà là 100 triệu đồng/nhà chòi. Công ty chỉ trả được 30% tổng chi phí xây dựng 24 nhà chòi đó. Số tiền còn thiếu, công ty phải vay ngân hàng với lãi suất 10%/năm (với thể thức lãi kép, lãi suất không thay đổi trong thời gian vay). Sau đúng 5 năm, công ty trả nợ ngân hàng cả gốc và lãi với số tiền là (làm tròn đến hàng ngàn)

A. 3 456 123 000 đồng.

B. 5 255 678 000 đồng.

C. 7 508 112 000 đồng.

D. 2 252 434 000 đồng.

Xem lời giải

Câu hỏi trong đề: Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 6) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi r, h, l lần lượt là bán kính đáy, chiều cao và độ dài đường sinh của mái nhà chòi.

\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{r = 3\;{\rm{m}}}\\{h = 4\;{\rm{m}}}\end{array} \Rightarrow l = \sqrt {{r^2} + {h^2}} = \sqrt {{3^2} + {4^2}} = 5\;{\rm{m}}} \right.{\rm{.}}\)

\( \Rightarrow \) Diện tích xung quanh của mái một nhà chòi là \({S_{xq}} = \pi rl = \pi .3.5 = 15\pi \,\,\left( {{{\rm{m}}^2}} \right)\).

\( \Rightarrow \) Tổng chi phí xây dựng 24 căn nhà chòi là

\(P = 24.\left( {2.{S_{xq}} + 100} \right){.10^6} = 24.(2.15\pi + 100){.10^6} = (72\pi + 240){.10^7}\) (đồng).

\( \Rightarrow \) Số tiền công ty còn thiếu là \({A_0} = 70\% .P = (504\pi + 1680){.10^6}\) (đồng).

Sau năm thứ nhất, số tiền công ty nợ ngân hàng là

\({S_1} = {A_0} + {A_0}.10\% = {A_0}(1 + 10\% )\)

Sau năm thứ hai, số tiền công ty nợ ngân hàng là

\({S_2} = {S_1} + {S_1}.10\% = {S_1}(1 + 10\% ) = {A_0}(1 + 10\% )(1 + 10\% ) = {A_0}{(1 + 10\% )^2}{\rm{. }}\)

...

Sau 5 năm, số tiền công ty phải trả nợ ngân hàng cả gốc lẫn lãi là

\({S_5} = {A_0}{(1 + 10\% )^5} = (504\pi + 1680).{(1 + 10\% )^5}{.10^6} \approx 5255678000\) (đồng).

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một vật đang chuyển động đều với vận tốc v0(m/s) thì bắt đầu tăng tốc với phương trình gia tốc \(a(t) = {v_0}t + {t^2}\left( {{\rm{m}}/{{\rm{s}}^2}} \right)\) trong đó t là khoảng thời gian được tính bằng giây kể từ thời điểm vật bắt đầu tăng tốc. Biết quãng đường vật đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng tốc là 100 m. Khi đó, vận tốc ban đầu v0 của vật bằng bao nhiêu (làm tròn đến chữ số thập phân thứ 3)?

A. 20,722 (m/s).

B. 12,433 (m/s)

C. 21,722 (m/s).

D. 13,433 (m/s).

Lời giải

Phương trình vận tốc \(v(t) = \int a (t){\rm{d}}t = \int {\left( {{v_0}t + {t^2}} \right)} dt = {v_0}\frac{{{t^2}}}{2} + \frac{{{t^3}}}{3} + C\)

Tại thời điểm \(t = 0 \Rightarrow v(t) = {v_0} \Rightarrow C = {v_0}\)

Vì quãng đường vật đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng tốc là 100 m nên

\(S = 100 = \int\limits_0^3 {v(t)} {\rm{d}}t = \int\limits_0^3 {\left( {{v_0}\frac{{{t^2}}}{2} + \frac{{{t^3}}}{3} + {v_0}} \right)} {\rm{d}}t = 3{v_0} + \frac{9}{2}{v_0} + \frac{{27}}{4} \Rightarrow {v_0} = 12,433\) m/s.

Câu 2

Theo thống kê tại một nhà máy Z, nếu áp dụng tuần làm việc 40 giờ thì mỗi tuần có 100 công nhân đi làm và mỗi công nhân làm được 120 sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm 2 giờ mỗi tuần thì sẽ có 1 công nhân nghỉ việc và năng suất lao động giảm 5 sản phẩm/1 công nhân/1 giờ. Ngoài ra, số phế phẩm mỗi tuần ước tính là \(P(x) = \frac{{95{x^2} + 120x}}{4}\), với x là thời gian làm việc trong một tuần. Nhà máy cần áp dụng thời gian làm việc mỗi tuần (1) _______ giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất.

Xem đáp án

Lời giải

Theo thống kê tại một nhà máy Z, nếu áp dụng tuần làm việc 40 giờ thì mỗi tuần có 100 công nhân đi làm và mỗi công nhân làm được 120 sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm 2 giờ mỗi tuần thì sẽ có 1 công nhân nghỉ việc và năng suất lao động giảm 5 sản phẩm/1 công nhân/1 giờ. Ngoài ra, số phế phẩm mỗi tuần ước tính là \(P(x) = \frac{{95{x^2} + 120x}}{4}\), với x là thời gian làm việc trong một tuần. Nhà máy cần áp dụng thời gian làm việc mỗi tuần (1) __ 36 __ giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất.

Giải thích

Gọi \(t\) là số giờ làm tăng thêm mỗi tuần, \(t \in \mathbb{R}\)

\( \Rightarrow \) số công nhân bỏ việc là \(\frac{t}{2}\) nên số công nhân làm việc là \(100 - \frac{t}{2}\) người.

Năng suất của công nhân còn \(120 - \frac{{5t}}{2}\) sản phẩm một giờ.

Số thời gian làm việc một tuần là \(40 + t\) giờ.

Để nhà máy hoạt động được thì \(\left\{ {\begin{array}{*{20}{l}}{40 + t > 0}\\{120 - \frac{{5t}}{2} > 0 \Rightarrow t \in ( - 40;48){\rm{. }}}\\{100 - \frac{t}{2} > 0}\end{array}} \right.\)

Số sản phẩm trong một tuần làm được: \(S = \left( {100 - \frac{t}{2}} \right)\left( {120 - \frac{{5t}}{2}} \right)(40 + t)\).

Số sản phẩm thu được là

\(f(t) = \left( {100 - \frac{t}{2}} \right)\left( {120 - \frac{{5t}}{2}} \right)(40 + t) - \frac{{95{{(40 + t)}^2} + 120(40 + t)}}{4} = \frac{5}{4}{t^3} - \frac{{1135}}{4}{t^2} - 2330t + 440800.\)

\( \Rightarrow {f^\prime }(t) = = \frac{{15}}{4}{t^2} - \frac{{1135}}{2}t - 2330.\)

\({f^\prime }(t) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = - 4\,\,\,\,\,\,\,\,\,\,\,}\\{t = \frac{{466}}{3}\,\,(\;{\rm{L}})}\end{array}} \right.\)

Ta có BBT như sau

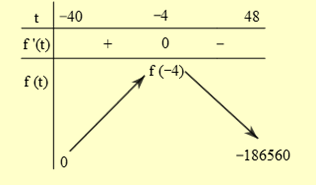
Media VietJack