Trong một hội thảo của công ty A gồm 100 người có cơ cấu theo trình độ cán bộ công nhân viên (CBCNV) như biểu đồ dưới đây:
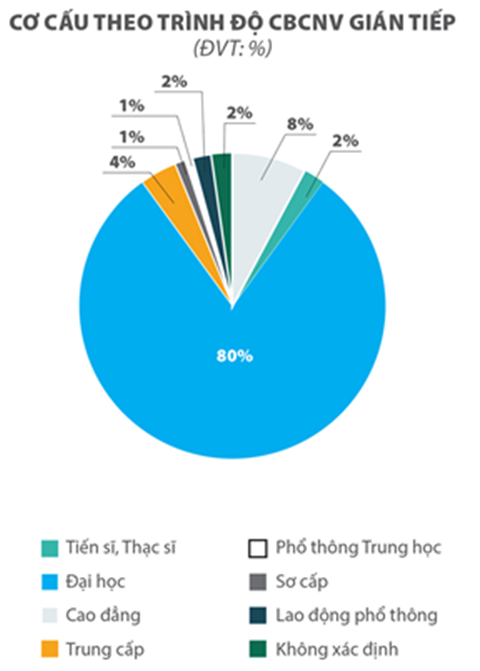
Chọn ra 20 người để nhận phần quà may mắn từ diễn giả của hội thảo. Xác suất để trong 20 người có \(\frac{3}{4}\) số người có trình độ là Đại học là bao nhiêu? (Kết quả làm tròn đến chữ số thập phân thứ hai)
Trong một hội thảo của công ty A gồm 100 người có cơ cấu theo trình độ cán bộ công nhân viên (CBCNV) như biểu đồ dưới đây:
Chọn ra 20 người để nhận phần quà may mắn từ diễn giả của hội thảo. Xác suất để trong 20 người có \(\frac{3}{4}\) số người có trình độ là Đại học là bao nhiêu? (Kết quả làm tròn đến chữ số thập phân thứ hai)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Giải thích
Trong hội nghị có 100 người nên \[n\left( \Omega \right) = C_{100}^{20}\]
+ Số người có trình độ là Đại học là: 100.80 (người).
Trong 20 người được nhận quà của diễn giả: có \(\frac{3}{4}\) số người có trình độ là Đại học và còn lại là các trình độ khác nên số cách chọn 20 người lên nhận quà là: \(n(A) = C_{80}^{15}.C_{20}^5\).
Xác suất cần tìm của đề bài là: \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{C_{80}^{15}.C_{20}^5}}{{C_{100}^{20}}} \approx 0,19.\)
Chọn A
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Nhiệt độ của chênh lệch giữa cốc nước và nhiệt độ ngăn mát tủ lạnh sau khoảng thời gian t là hàm số có dạng \(y(t) = y(0){e^{kt}}\). |
X | |
|
Kết quả làm tròn đến chữ số thập phân thứ tư của k là −0,0145. |
X | |
|
Sau 60 phút trong tủ lạnh, nhiệt độ của cốc nước khoảng 10∘C (Kết quả làm tròn đến chữ số hàng đơn vị). |
X |
Giải thích
|
Lí do lựa chọn phương án |
1) |
Đúng vì: Do \(\frac{{y'(t)}}{{y(t)}} = k\) với k là hằng số. Lấy tích phân với cận từ 0 đến t hai vế. Ta được \(\int_0^t {\frac{{y'(t)}}{{y(t)}}} dt = \int_0^t k dt\) Kéo theo \(\ln \frac{{y(t)}}{{y(0)}} = kt\), hay \(y(t) = y(0).{e^{kt}}\). |
|
2) |
Đúng vì: Tính được \[y(0) = T(0) - {T_s} = 22 - 5 = 17\]. Ta có \(T(t) = {T_s} + y(t) = 5 + 17{e^{kt}}\). Thay t = 30 ta được \(T(30) = 5 + 17{e^{30k}}\). Mà \(T(30) = 16\) nên \(k = \ln \left( {\frac{{11}}{{17}}} \right):30 \approx - 0,0145\). |
|
|
3) |
Sai vì: Tính \(T(60) \approx 12\) (Kết quả làm tròn đến chữ số hàng đơn vị). |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án
Trong không gian Oxyz, cho 2 vectơ \(\vec a,\vec b\) tạo với nhau góc \({120^o}\) và \(|\vec a| = 3;|\vec b| = 5\). Giá trị của \(T = |\vec a - \vec b|\) bằng (1) __ 7 __ .
Giải thích
Ta có \({T^2} = |\vec a - \vec b{|^2} = {\vec a^2} + {\overrightarrow b ^2} - 2\vec a.\vec b \Leftrightarrow {T^2} = {\vec a^2} + {\overrightarrow b ^2} - 2.|\vec a|.|\vec b|.\cos (\vec a,\vec b)\)
\( \Leftrightarrow {T^2} = {3^2} + {5^2} - 2.3.5.\cos {120^^\circ } \Leftrightarrow {T^2} = 49 \Rightarrow T = 7.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập