Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai số phức \({z_1}\) có điểm biểu diễn \(M\), số phức \({z_2}\) có điểm biểu diễn là \(N\) thỏa mãn \(\left| {{z_1}} \right| = 1,\left| {{z_2}} \right| = 3\) và \(\widehat {MON} = {120^o }\). Giá trị lớn nhất của \(\left| {3{z_1} + 2{z_2} - 3i} \right|\) là \({M_0}\), giá trị nhỏ nhất của \(\left| {3{{\rm{z}}_1} - 2{z_2} + 1 - 2i} \right|\) là \({m_0}\). Biết \({M_0} + {m_0} = a\sqrt 7  + b\sqrt 5  + c\sqrt 3  + d\), với \(a,b,c,d \in \mathbb{Z}.a + b + c + d = \) (1) ________

Đáp án

Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai số phức \({z_1}\) có điểm biểu diễn \(M\), số phức \({z_2}\) có điểm biểu diễn là \(N\) thỏa mãn \(\left| {{z_1}} \right| = 1,\left| {{z_2}} \right| = 3\) và \(\widehat {MON} = {120^o }\). Giá trị lớn nhất của \(\left| {3{z_1} + 2{z_2} - 3i} \right|\) là \({M_0}\), giá trị nhỏ nhất của \(\left| {3{{\rm{z}}_1} - 2{z_2} + 1 - 2i} \right|\) là \({m_0}\). Biết \({M_0} + {m_0} = a\sqrt 7  + b\sqrt 5  + c\sqrt 3  + d\), với \(a,b,c,d \in \mathbb{Z}.a + b + c + d = \) (1) __ 8 __ 

Giải thích

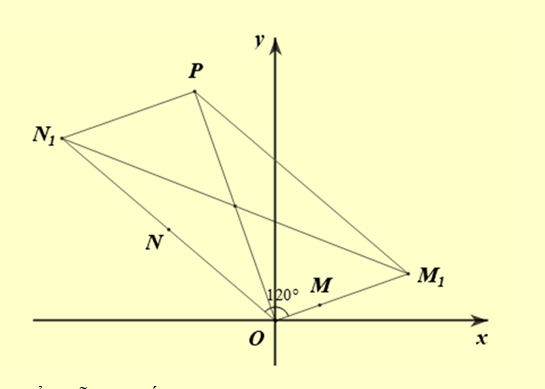
Gọi \({M_1}\) là điểm biểu diễn của số phức \(3{z_1}\), suy ra \(O{M_1} = 3\).

Gọi \({N_1}\) là điểm biểu diễn của số phức \(2{z_2}\), suy ra \(O{N_1} = 6\). Gọi \(P\) là điểm sao cho

\(\overrightarrow {O{M_1}}  + \overrightarrow {O{N_1}}  = \overrightarrow {OP} \). Suy ra tứ giác \(O{M_1}P{N_1}\) là hình bình hành.

Do từ giả thiết \(\widehat {MON} = {120^o }\), suy ra \({\widehat {{M_1}ON}_1} = {120^o } \Rightarrow \widehat {O{M_1}P} = {60^o }\).

Dùng định lí cosin trong tam giác \(O{M_1}{N_1}\) ta tính được \({M_1}{N_1} = \sqrt {9 + 36 - 2.3.6.\left( { - \frac{1}{2}} \right)}  = 3\sqrt 7 \);

và định lí cosin trong tam giác \(O{M_1}P\) ta có \(OP = \sqrt {9 + 36 - 2.3.6.\frac{1}{2}}  = 3\sqrt 3 \).

Ta có \({M_1}{N_1} = \left| {3{z_1} - 2{z_2}} \right| = 3\sqrt 7 ;OP = \left| {3{z_1} + 2{z_2}} \right| = 3\sqrt 3 \).

Tìm giá trị lớn nhất của \(\left| {3{{\rm{z}}_1} + 2{z_2} - 3i} \right|\).

Đặt \(3{z_1} + 2{z_2} = {w_1} \Rightarrow \left| {{w_1}} \right| = 3\sqrt 3 \), suy ra điểm biểu diễn \({w_1}\) là \(A\) thuộc đường tròn \(\left( {{C_1}} \right)\) tâm \(O(0;0)\) bán kính \({R_1} = 3\sqrt 3 \). Gọi điểm \({Q_1}\) là biểu diễn số phức 3i.

Khi đó \(\left| {3{{\rm{z}}_1} + 2{z_2} - 3i} \right| = A{Q_1}\), bài toán trở thành tìm \({\left( {A{Q_1}} \right)_{\max }}\) biết điểm \(A\) trên đường tròn \(\left( {{C_1}} \right)\).

Dễ thấy \({\left( {A{Q_1}} \right)_{\max }} = O{Q_1} + {R_1} = 3 + 3\sqrt 3 \).

Tìm giá trị nhỏ nhất của \(\left| {3{{\rm{z}}_1} - 2{z_2} + 1 - 2i} \right| = \left| {3{{\rm{z}}_1} - 2{z_2} - ( - 1 + 2i)} \right|\).

Đặt \(3{z_1} - 2{z_2} = {w_2} \Rightarrow \left| {{w_2}} \right| = 3\sqrt 7 \), suy ra điểm biểu diễn \({w_2}\) là \(B\) thuộc đường tròn \(\left( {{C_2}} \right)\) tâm \(O(0;0)\) bán kính \({R_1} = 3\sqrt 7 \). Gọi điểm \({Q_2}\) là biểu diễn số phức \( - 1 + 2i\).

Khi đó \(\left| {3{{\rm{z}}_1} - 2{z_2} - ( - 1 + 2i)} \right| = B{Q_2}\), bài toán trở thành tìm \({\left( {B{Q_2}} \right)_{\min }}\) biết điểm \(B\) trên đường tròn \(\left( {{C_2}} \right)\).

Dễ thấy điểm \({Q_2}\) nằm trong đường tròn \(\left( {{C_2}} \right)\) nên \({\left( {B{Q_2}} \right)_{\min }} = {R_2} - O{Q_2} = 3\sqrt 7  - \sqrt 5 \).

Vậy \({M_0} + {m_0} = 3\sqrt 7  + 3\sqrt 3  - \sqrt 5  + 3\).

Suy ra \(a + b + c + d = 8\).