Cho hình chóp S.ABCD có đáy là hình vuông cạnh 8 , mặt bên SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ \(B\) đến mặt phẳng \((SAC)\) là \(\frac{{a\sqrt b }}{c}\) (phân số tối giản với \(c > 0)\). Tính \(a + {b^2} - {c^3}\).
A. −485.
B. −214.
C. 106.
D. 203.
Quảng cáo
Trả lời:
Giải bởi Vietjack
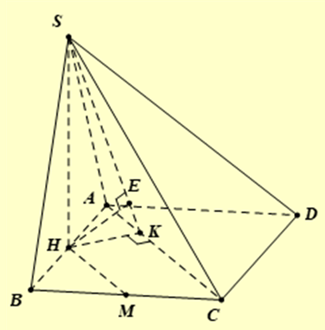
Kẻ \(SH \bot AB \Rightarrow H\) là trung điểm của AB.
Do \((SAB) \bot (ABCD)\) và \((SAB) \cap (ABCD) = AB\) nên từ \(SH \bot AB\) ta được \(SH \bot (ABCD)\).
Mặt khác ta có \(B\dot A \cap (SAC) = \{ A\} \) và \(H\) là trung điểm của AB nên ta có \(d(B,(SAC)) = 2d(H,(SAC))\).
Trong \((ABCD)\) kẻ \(HK \bot AC\,\,(K \in AC)\) và trong \((SHK)\) kẻ \(HE \bot SK(E \in SK)\).
Ta có: \(SH \bot (ABCD) \Rightarrow SH \bot AC\). Kết hợp với \(HK \bot AC\) ta được \(AC \bot (SHK) \Rightarrow AC \bot HE\).
Hơn nữa \(HE \bot SK\) nên \(HE \bot (SAC)\).
Vậy \(d(H,(SAC)) = HE \Rightarrow d(B,(SAC)) = 2HE\).
Trong \((ABCD)\) ta có .
Mặt khác do \(\Delta SAB\) đều nên \(SH = \frac{{8\sqrt 3 }}{2} = 4\sqrt 3 \). Áp dụng hệ thức lượng trong \(\Delta SHK\) ta có
\(\frac{1}{{H{E^2}}} = \frac{1}{{H{K^2}}} + \frac{1}{{S{H^2}}} \Rightarrow HE = \frac{{4\sqrt {21} }}{7} \Rightarrow d(B,(SAC)) = \frac{{8\sqrt {21} }}{7}\). Suy ra \(a = 8,b = 21,c = 7\).
Vậy \(a + {b^2} - {c^3} = 106\).
Chọn C
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án
Trong không gian Oxyz, cho 2 vectơ \(\vec a,\vec b\) tạo với nhau góc \({120^o}\) và \(|\vec a| = 3;|\vec b| = 5\). Giá trị của \(T = |\vec a - \vec b|\) bằng (1) __ 7 __ .
Giải thích
Ta có \({T^2} = |\vec a - \vec b{|^2} = {\vec a^2} + {\overrightarrow b ^2} - 2\vec a.\vec b \Leftrightarrow {T^2} = {\vec a^2} + {\overrightarrow b ^2} - 2.|\vec a|.|\vec b|.\cos (\vec a,\vec b)\)
\( \Leftrightarrow {T^2} = {3^2} + {5^2} - 2.3.5.\cos {120^^\circ } \Leftrightarrow {T^2} = 49 \Rightarrow T = 7.\)
Lời giải
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Nhiệt độ của chênh lệch giữa cốc nước và nhiệt độ ngăn mát tủ lạnh sau khoảng thời gian t là hàm số có dạng \(y(t) = y(0){e^{kt}}\). |
X | |
|
Kết quả làm tròn đến chữ số thập phân thứ tư của k là −0,0145. |
X | |
|
Sau 60 phút trong tủ lạnh, nhiệt độ của cốc nước khoảng 10∘C (Kết quả làm tròn đến chữ số hàng đơn vị). |
X |
Giải thích
|
Lí do lựa chọn phương án |
1) |
Đúng vì: Do \(\frac{{y'(t)}}{{y(t)}} = k\) với k là hằng số. Lấy tích phân với cận từ 0 đến t hai vế. Ta được \(\int_0^t {\frac{{y'(t)}}{{y(t)}}} dt = \int_0^t k dt\) Kéo theo \(\ln \frac{{y(t)}}{{y(0)}} = kt\), hay \(y(t) = y(0).{e^{kt}}\). |
|
2) |
Đúng vì: Tính được \[y(0) = T(0) - {T_s} = 22 - 5 = 17\]. Ta có \(T(t) = {T_s} + y(t) = 5 + 17{e^{kt}}\). Thay t = 30 ta được \(T(30) = 5 + 17{e^{30k}}\). Mà \(T(30) = 16\) nên \(k = \ln \left( {\frac{{11}}{{17}}} \right):30 \approx - 0,0145\). |
|
|
3) |
Sai vì: Tính \(T(60) \approx 12\) (Kết quả làm tròn đến chữ số hàng đơn vị). |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(c < a < b\).
B. \(b < a < c\).
C. \(c < b < a\).
D. \(a < c < b\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. càng nhiều nhiệt lượng nhận từ nguồn nhiệt Q1 chuyển thành công càng tốt.
B. càng nhiều nhiệt lượng nhận từ nguồn nhiệt Q2 chuyển thành công càng tốt.
C. càng nhiều nhiệt lượng lấy từ nguồn nhiệt Q1 chuyển sang nguồn nhiệt Q2 càng tốt.
D. càng nhiều nhiệt lượng lấy từ nguồn nhiệt Q2 chuyển sang nguồn nhiệt Q1 càng tốt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 3.
B. 2.
C. \(\frac{5}{6}\).
D. \(\frac{3}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập