Câu hỏi:
23/10/2024 154
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau
Khoảng cách từ tâm mặt cầu (S) đến đường thẳng d bằng _______.
Mặt phẳng (P) chứa đường thẳng d và có khoảng cách từ tâm mặt cầu (S) tới mặt phẳng là lớn nhất có phương trình \[ax + by + cz = 18\] với a = _______ ; b = _______; c = _______.
Khoảng cách từ tâm mặt cầu (S) đến đường thẳng d bằng _______.
Mặt phẳng (P) chứa đường thẳng d và có khoảng cách từ tâm mặt cầu (S) tới mặt phẳng là lớn nhất có phương trình \[ax + by + cz = 18\] với a = _______ ; b = _______; c = _______.
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa... kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 70k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
Khoảng cách từ tâm mặt cầu (S) đến đường thẳng d bằng \(\sqrt 5 \) .
Mặt phẳng (P) chứa đường thẳng d và có khoảng cách từ tâm mặt cầu (S) tới mặt phẳng là lớn nhất có phương trình \[ax + by + cz = 18\] với a = 5 ; b = 2 ; c = 4 .
Giải thích
Mặt cầu \((S)\) có tâm \(I(1; - 1;0)\), bán kính \(R = 2\).
Đường thẳng \(d\) có vecto chỉ phương \(\vec u = ( - 2;1;2)\) và điểm \(M(4; - 1;0) \in d\).
\(\overrightarrow {IM} = (3;0;0) \Rightarrow [\overrightarrow {IM} ;\vec u] = (0; - 6;3) \Rightarrow d(I;d) = \frac{{\left| {\left[ {\overrightarrow {IM} ;\vec u} \right]} \right|}}{{|\vec u|}} = \sqrt 5 \)
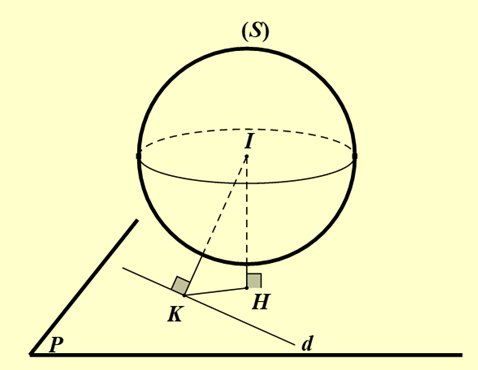
Gọi H, K lần lượt là hình chiếu của \(I\) trên mặt phẳng \((P)\) và đường thẳng \(d\).
Khi đó, \(IH \le IK \Rightarrow I{H_{\max }} = IK = d(I;d) = \sqrt 5 \).
Mặt phẳng \((\alpha )\) đi qua điểm \(I(1; - 1;0)\) và nhận \(\vec u = ( - 2;1;2)\) làm vecto pháp tuyến có phương trình: \( - 2(x - 1) + (y + 1) + 2z = 0 \Leftrightarrow 2x - y - 2z - 3 = 0\).
\( \Rightarrow K = d \cap (\alpha ) \Rightarrow \) Tọa độ điểm \(K\) thỏa mãn hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{\frac{{x - 4}}{{ - 2}} = \frac{{y + 1}}{1} = \frac{z}{2}}\\{2x - y - 2z - 3 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \frac{8}{3}}\\{y = - \frac{1}{3}}\\{z = \frac{4}{3}}\end{array}} \right.} \right.\) \( \Rightarrow K\left( {\frac{8}{3}; - \frac{1}{3};\frac{4}{3}} \right) \Rightarrow \overrightarrow {IK} = \left( {\frac{5}{3};\frac{2}{3};\frac{4}{3}} \right)\).
Mặt phẳng \((P)\) đi qua điểm \(M(4; - 1;0)\) và nhận vecto \(\vec n(5;2;4)\) làm vecto pháp tuyến có phương trình: \(5(x - 4) + 2(y + 1) + 4z = 0 \Leftrightarrow 5x + 2y + 4z - 18 = 0\).
Nhà sách VIETJACK:
Sách - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) cho 2k7 VietJack
Đã bán 851
₫ 150.000
₫ 39.000
Sách Combo - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) - 2024 cho 2k7 VietJack
Đã bán 1,4k
₫ 290.000
₫ 140.000
Sách - Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) cho 2k7 VietJack
Đã bán 902
₫ 150.000
₫ 39.000
Sách Combo - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) - 2024 cho 2k7 VietJack
Đã bán 1,4k
₫ 280.000
₫ 150.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian Oxyz, cho 2 vectơ \(\vec a,\vec b\) tạo với nhau góc \({120^o }\) và \(|\vec a| = 3;|\vec b| = 5\). Giá trị của \(T = |\vec a - \vec b|\) bằng (1) _______.
Trong không gian Oxyz, cho 2 vectơ \(\vec a,\vec b\) tạo với nhau góc \({120^o }\) và \(|\vec a| = 3;|\vec b| = 5\). Giá trị của \(T = |\vec a - \vec b|\) bằng (1) _______.
Xem đáp án »
23/10/2024
2,571
Câu 2:
Khẳng định nào sau đây là đúng? Một động cơ nhiệt hoạt động tốt có nghĩa là
Xem đáp án »
30/06/2024
1,467
Câu 3:
Cho ba số \(a = {1000^{1001}},b = {2^{{2^{64}}}}\) và \(c = {1^1} + {2^2} + {3^3} + \ldots + {1000^{1000}}\).
Xem đáp án »
23/10/2024
1,385
Câu 4:
Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'(x) = {x^2}(x + 2)(x - 3)\).
Mỗi phát biểu sau đây là đúng hay sai?
Phát biểu
Đúng
Sai
Hàm số \(f(x)\) có 3 điểm cực trị.
Hàm số \(f(x)\) nghịch biến trên (-2;3).
Hàm số \(f(x)\) có điểm cực đại là x = 2.
Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'(x) = {x^2}(x + 2)(x - 3)\).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Hàm số \(f(x)\) có 3 điểm cực trị. |
||
|
Hàm số \(f(x)\) nghịch biến trên (-2;3). |
||
|
Hàm số \(f(x)\) có điểm cực đại là x = 2. |
Xem đáp án »
23/10/2024
1,210
Câu 5:
Phát biểu sau đúng hay sai?
Hợp chất hữu cơ X có phần trăm khối lượng của các nguyên tố như sau: %C = 45,80%; %H = 10,57%; %N = 13,24%, còn lại là O. Biết MC =12,01 g/mol, MH = 1,008 g/mol và MO = 16,00 g/mol. Công thức kinh nghiệm của X là C4H10NO2.
Phát biểu sau đúng hay sai?
Hợp chất hữu cơ X có phần trăm khối lượng của các nguyên tố như sau: %C = 45,80%; %H = 10,57%; %N = 13,24%, còn lại là O. Biết MC =12,01 g/mol, MH = 1,008 g/mol và MO = 16,00 g/mol. Công thức kinh nghiệm của X là C4H10NO2.
Xem đáp án »
30/06/2024
1,019
Câu 6:
Cho \(\log _2^2(xy) = {\log _2}\left( {\frac{x}{4}} \right){\log _2}(4y)\). Biểu thức \(P = {\log _3}(x + 4y + 4) + {\log _2}(x - 4y - 1)\) có giá trị bằng bao nhiêu?
Xem đáp án »
23/10/2024
923
Câu 7:
Phát biểu sau đúng hay sai?
Phương trình phản ứng xảy ra trong thí nghiệm 2 là: 2H2+O2→2H2O.
Phát biểu sau đúng hay sai?
Phương trình phản ứng xảy ra trong thí nghiệm 2 là: 2H2+O2→2H2O.
Xem đáp án »
30/06/2024
910
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Top 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2023 - 2024 có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 3)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 15)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận