Câu hỏi:
24/10/2024 273
Cho hàm số \(f\left( x \right) = \left( {m - 1} \right){x^3} + 2m{x^2} + 1\), với \(m\) là tham số.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Với \(m = \)_______, hàm số đã cho có một điểm cực trị.
Có _______ giá trị nguyên của tham số \(m\) thuộc \(\left[ { - 10;10} \right]\) để \(\mathop {{\rm{max}}}\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( 3 \right)\).
Cho hàm số \(f\left( x \right) = \left( {m - 1} \right){x^3} + 2m{x^2} + 1\), với \(m\) là tham số.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Với \(m = \)_______, hàm số đã cho có một điểm cực trị.
Có _______ giá trị nguyên của tham số \(m\) thuộc \(\left[ { - 10;10} \right]\) để \(\mathop {{\rm{max}}}\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( 3 \right)\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
Với \(m = \)1 , hàm số đã cho có một điểm cực trị.
Có 10 giá trị nguyên của tham số \(m\) thuộc \(\left[ { - 10;10} \right]\) để \(\mathop {{\rm{max}}}\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( 3 \right)\).
Giải thích
Để hàm số có một điểm cực trị thì \(m - 1 = 0 \Leftrightarrow m = 1\). Khi đó \(f\left( x \right) = 2{x^2} + 1\) (thỏa mãn có 1 điểm cực trị).
Với \(m = 1\) ta có: \(f\left( x \right) = 2{x^2} + 1\).
Vì hàm số \(f\left( x \right) = 2{x^2} + 1\) là hàm số chẵn nên nhận trục \(Oy\) làm trục đối xứng
\( \Rightarrow \mathop {{\rm{max}}}\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( 3 \right)\)
Với \(m \ne 1\) ta có: \(f'\left( x \right) = 3\left( {m - 1} \right){x^2} + 4mx;f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x_1} = 0}\\{{x_2} = \frac{{4m}}{{3\left( {1 - m} \right)}}}\end{array}} \right.\)
Xét \({x_2} < {x_1} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m > 1}\\{m < 0}\end{array}} \right.\), ta có bảng biến thiên của hàm số \(y = f\left( x \right)\) như sau:
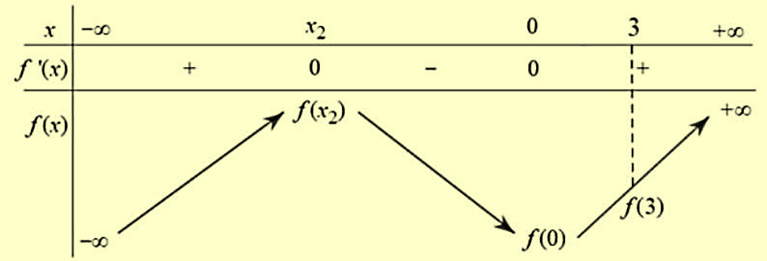
Để \(\mathop {{\rm{max}}}\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( 3 \right)\) thì \(\left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{{x_2} < - 2}\\{f\left( { - 2} \right) \le f\left( 3 \right)}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{ - 2 \le {x_2}}\\{f\left( {{x_2}} \right) \le f\left( 3 \right)}\end{array}} \right.}\end{array}} \right.\)
\(\) \[ \Leftrightarrow \left[ \begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{\frac{{4m}}{{3(1 - m)}} < - 2}\\{9 \le 45m - 26}\end{array}} \right.\\\left\{ \begin{array}{l}\frac{{4m}}{{3(1 - m)}} \ge - 2\\\frac{{32{m^3}}}{{27{{(m - 1)}^2}}} + 1 \le 45m - 26\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{1 < m < 3}\\{m > \frac{7}{9}}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{\left[ {\begin{array}{*{20}{l}}{m \ge 3}\\{m \le 1}\end{array}} \right.}\\{\left[ {\begin{array}{*{20}{l}}{m = \frac{9}{{13}}}\\{m \ge \frac{9}{7}}\end{array}} \right.}\end{array}} \right.\end{array} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{1 < m < 3}\\{m \ge 3}\\{m = \frac{9}{{13}}}\end{array}} \right.\] (thỏa mãn điều kiện)
Xét \({x_2} > {x_1} \Leftrightarrow 0 < m < 1\), ta có bảng biến thiên của hàm số \(y = f\left( x \right)\) như sau:
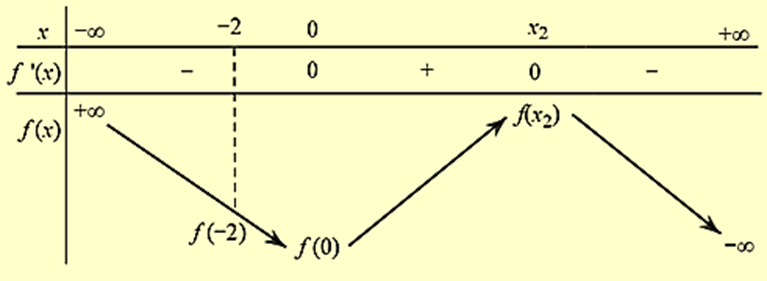
Để thì \(\left\{ {\begin{array}{*{20}{c}}{{x_2} \ge 3}\\{f\left( { - 2} \right) \le f\left( 3 \right)}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{4m}}{{3\left( {1 - m} \right)}} \ge 3}\\{9 \le 45m - 26}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{9}{{13}} \le m < 1}\\{m \le \frac{7}{9}}\end{array} \Leftrightarrow \frac{7}{9} \le m < 1} \right.} \right.\) (thỏa mãn điều kiện)
Kết hợp các trường hợp và \(m \in \left[ { - 10;10} \right],m \in \mathbb{Z}\) nên \(m \in \left\{ {1;2; \ldots ;10} \right\}\).
Nhà sách vietjack
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Trên tập số thực, cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu là \(\frac{1}{2}\), số hạng thứ tư là 32 và số hạng cuối là 2048. Tính tổng \(T\) các số hạng của cấp số nhân đã cho.
Xem đáp án »
24/10/2024
1,510
Câu 3:
Virus nhận ra các tế bào chủ của nó theo nguyên tắc “chìa và khóa” nghĩa là
Virus nhận ra các tế bào chủ của nó theo nguyên tắc “chìa và khóa” nghĩa là
Xem đáp án »
01/07/2024
1,472
Câu 4:
Phần tư duy đọc hiểu
Hãy điền một cụm từ không quá hai tiếng để hoàn thành câu văn sau:
Trong sự phát triển của đời sống, giới trẻ ngày nay có xu hướng (1) ______ hình thức giải trí sang các hoạt động trực tuyến thay vì đọc sách, báo in như thập niên trước.
Phần tư duy đọc hiểu
Hãy điền một cụm từ không quá hai tiếng để hoàn thành câu văn sau:
Trong sự phát triển của đời sống, giới trẻ ngày nay có xu hướng (1) ______ hình thức giải trí sang các hoạt động trực tuyến thay vì đọc sách, báo in như thập niên trước.
Xem đáp án »
13/07/2024
1,453
Câu 5:
Xung quanh một bờ hồ hình tròn có trồng 20 cây cau cảnh. Người ta dự định chặt bớt 5 cây sao cho không có hai cây nào kề nhau bị chặt. Có (1) ______ cách thực hiện khác nhau.
Xung quanh một bờ hồ hình tròn có trồng 20 cây cau cảnh. Người ta dự định chặt bớt 5 cây sao cho không có hai cây nào kề nhau bị chặt. Có (1) ______ cách thực hiện khác nhau.
Xem đáp án »
24/10/2024
1,428
Câu 6:
Phần tư duy khoa học / giải quyết vấn đề
Hãy hoàn thành nhận định sau đây bằng cách kéo thả các từ vào đúng vị trí
lớn hơn, nhỏ hơn
Gia tốc trọng trường trên bề mặt Trái Đất _______ gia tốc trọng trường trên bề mặt Mặt Trăng.
Gia tốc trọng trường trên bề mặt Trái Đất _______ gia tốc trọng trường trên bề mặt Sao Mộc.
Xem đáp án »
13/07/2024
1,170
Câu 7:
Phát biểu sau đây đúng hay sai?
Theo thí nghiệm 1, phân lập B có số lượng vi khuẩn phát triển lớn nhất khi được cung cấp nguồn carbon là galactose.
Phát biểu sau đây đúng hay sai?
Theo thí nghiệm 1, phân lập B có số lượng vi khuẩn phát triển lớn nhất khi được cung cấp nguồn carbon là galactose.
Xem đáp án »
01/07/2024
1,049
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 15)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 3)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 5)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận