Có hai hộp đựng bi, các viên bi được đánh các số tự nhiên, trong đó hộp 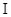 có
có  viên bi được đánh số
viên bi được đánh số 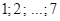 . Lấy ngẫu nhiên từ mỗi hộp một viên bi. Biết rằng xác suất để lấy được viên bi mang số lẻ ở hộp
. Lấy ngẫu nhiên từ mỗi hộp một viên bi. Biết rằng xác suất để lấy được viên bi mang số lẻ ở hộp 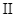 là
là  . Xác suất để lấy được cả hai viên bi lấy ra đều mang số lẻ là:
. Xác suất để lấy được cả hai viên bi lấy ra đều mang số lẻ là:
Quảng cáo
Trả lời:
Gọi ![]() là biến cố “Lấy được cả hai viên bi mang số lẻ”.
là biến cố “Lấy được cả hai viên bi mang số lẻ”.
Gọi ![]() là biến cố: “Lấy được viên bi mang số lẻ ở hộp
là biến cố: “Lấy được viên bi mang số lẻ ở hộp ![]() ”. Khi đó
”. Khi đó 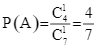 .
.
Gọi ![]() là biến cố: “Lấy được viên bi mang số lẻ ở hộp
là biến cố: “Lấy được viên bi mang số lẻ ở hộp ![]() ”. Theo đề bài
”. Theo đề bài ![]() .
.
Vì ![]() và
và ![]() là hai biến cố độc lập nên
là hai biến cố độc lập nên ![]() .
.
Theo công thức nhân xác suất ta có: ![]() . Chọn C.
. Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét các biến cố:
![]() : “Người được chọn mắc bệnh X”;
: “Người được chọn mắc bệnh X”;
![]() : “Người được chọn có phản ứng dương tính với xét nghiệm Y”.
: “Người được chọn có phản ứng dương tính với xét nghiệm Y”.
Theo giả thiết ta có: ![]() ;
; ![]() .
.
Theo công thức Bayes, ta có:
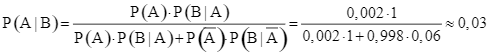 .
.
Vậy nếu người được chọn có phản ứng dương tính với xét nghiệm Y thì xác suất bị mắc bệnh X của người đó là khoảng 0,03. Chọn D.
Lời giải
Hình hộp có đáy là hình vuông cạnh ![]() (cm).
(cm).
Chiều cao của hình hộp là ![]() (cm). Thể tích hình hộp là
(cm). Thể tích hình hộp là ![]() (cm3).
(cm3).
Bài toán đưa về tìm ![]() để hàm số
để hàm số ![]() có giá trị lớn nhất.
có giá trị lớn nhất.
Ta có: ![]() .
.
![]() xác định
xác định ![]() ;
; ![]() hoặc
hoặc ![]() .
.
Bảng biến thiên của hàm số trên khoảng ![]() như sau:
như sau:
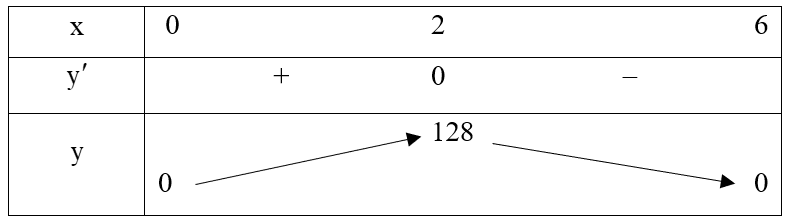
Hàm số đạt giá trị lớn nhất tại ![]() .
.
Đáp án cần nhập là: ![]() .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

