Câu hỏi:
29/10/2024 168
Đọc đoạn trích sau đây và trả lời câu hỏi:
Bắt đầu cầm bút, nhà văn đã từng đi đây đi đó: các tỉnh đồng bằng, trung du, và cả thượng du. Một số bài thơ có ghi rõ địa điểm sáng tác: Bắc Giang, Phú Thọ, Yên Bái, Lạng Sơn,..
Nguyễn Bính từng qua Huế. Ở miền Nam, nhà thơ cũng đi được nhiều nơi, nhất là những vùng nổi tiếng như Đồng bằng sông Cửu Long, các miệt vườn, cánh rừng miền Đông, các tỉnh thành phố lớn như đô thành Sài Gòn và vùng biển Tây như Rạch Giá, Hà Tiên,...
Sẽ rất thú vị nếu ta lập được một bản đồ in dấu chân nhà thơ. Kể về thú đi và viết thời ấy, Nguyễn Bính còn là hạng “đàn em” so với Nguyễn Tuân “có gen giang hồ” và “mắc bệnh xê dịch”.
(Trích Nguyễn Bính – người thơ, đời thơ – Đoàn Trọng Huy)
Đặt trong ngữ cảnh của cả đoạn, “gen giang hồ” trong câu cuối có nghĩa là:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Bắt đầu cầm bút, nhà văn đã từng đi đây đi đó: các tỉnh đồng bằng, trung du, và cả thượng du. Một số bài thơ có ghi rõ địa điểm sáng tác: Bắc Giang, Phú Thọ, Yên Bái, Lạng Sơn,..
Nguyễn Bính từng qua Huế. Ở miền Nam, nhà thơ cũng đi được nhiều nơi, nhất là những vùng nổi tiếng như Đồng bằng sông Cửu Long, các miệt vườn, cánh rừng miền Đông, các tỉnh thành phố lớn như đô thành Sài Gòn và vùng biển Tây như Rạch Giá, Hà Tiên,...
Sẽ rất thú vị nếu ta lập được một bản đồ in dấu chân nhà thơ. Kể về thú đi và viết thời ấy, Nguyễn Bính còn là hạng “đàn em” so với Nguyễn Tuân “có gen giang hồ” và “mắc bệnh xê dịch”.
(Trích Nguyễn Bính – người thơ, đời thơ – Đoàn Trọng Huy)
Đặt trong ngữ cảnh của cả đoạn, “gen giang hồ” trong câu cuối có nghĩa là:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Nguyễn Tuân từng nói: “Phải nói rằng họ nhà tôi có cái gien giang hồ. Gien di truyền nó là khoa học đấy! Không hiểu cụ tổ tôi thì thế nào chứ từ ông nội tôi, đến bố tôi và cho đến tôi thì cái gien giang hồ như ngày càng mạnh lên. Ông tôi và bố tôi là những người thích chu du đây đó, ra Bắc và Nam.”.
Đặt trong ngữ cảnh của cả đoạn, “gen giang hồ” trong câu cuối có nghĩa là thích chu du đây đó, có cuộc sống tự do, phóng túng. Chọn B.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét các biến cố:
: “Người được chọn mắc bệnh X”;
: “Người được chọn có phản ứng dương tính với xét nghiệm Y”.
Theo giả thiết ta có: 
; 
.
Theo công thức Bayes, ta có:
.
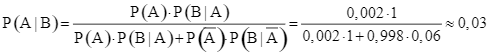Vậy nếu người được chọn có phản ứng dương tính với xét nghiệm Y thì xác suất bị mắc bệnh X của người đó là khoảng 0,03. Chọn D.
Lời giải
Hình hộp có đáy là hình vuông cạnh 
(cm).
Chiều cao của hình hộp là 
(cm). Thể tích hình hộp là 
(cm3).
Bài toán đưa về tìm 
để hàm số 
có giá trị lớn nhất.
Ta có: 
.
xác định 
; 
hoặc 
.
Bảng biến thiên của hàm số trên khoảng 
như sau:
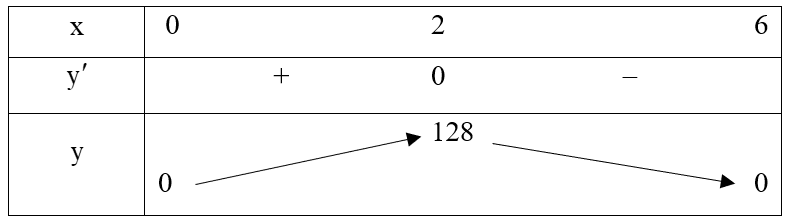
Hàm số đạt giá trị lớn nhất tại 
.
Đáp án cần nhập là: 
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo