Một bạn học sinh gieo đồng thời hai con xúc xắc cân đối, đồng chất liên tiếp 50 lần. Tổng số chấm xuất hiện trên hai con xúc xắc được thống kê trong bảng dưới đây:

Tổng số chấm	2	3	4	5	6	7	8	9	10	11	12
Số lần	0	3	4	5	7	5	8	9	3	4	2

Xác suất để tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn 7 bằng

Đáp án

Giải thích

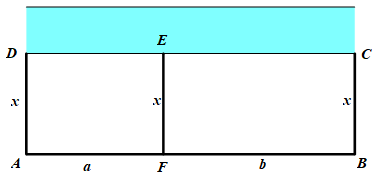
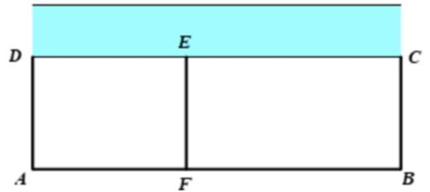
Gọi chiều rộng của hình chữ nhật là \(x\left( m \right){\rm{\;}}(x > 0)\) và chiều dài của phần đất trồng rau và nuôi gà lần lượt là \(a\left( m \right),b\left( m \right){\rm{\;}}(a > 0;b > 0)\).

Khi đó diện tích của khu đất là \(S = \left( {a + b} \right)x\left( {{m^2}} \right)\).

Mặt khác theo giả thiết tổng chi phí là 20 triệu đồng nên ta có:

\(3x.40000 + \left( {a + b} \right)80000 = 20000000 \Leftrightarrow 3x + 2\left( {a + b} \right) = 500\).

Ta có \(6S = 3x.2\left( {a + b} \right) \le \frac{{{{[3x + 2\left( {a + b} \right)]}^2}}}{4} = \frac{{{{500}^2}}}{4} \Rightarrow S \le \frac{{31250}}{3}\).

\( \Rightarrow {{\rm{S}}_{{\rm{max}}}} = \frac{{31250}}{3} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{a + b = 125}\\{x = \frac{{250}}{3}\,\,\,}\end{array}} \right.\)

\( \Rightarrow \) Chi phí nguyên vật liệu làm hàng rào \(AB\) là: \(125.80000 = 10000000\) (đồng).

Đáp án

Giải thích

Gọi \(M,N\) lần lượt là trung điểm của \(AB,AC;I\) là giao điểm của hai đường trung trực của hai đoạn thẳng \(AB\) và \(AC\).

Do \(M\) là trung điểm của cạnh huyền trong tam giác vuông \(AHB\) nên \(MA = MB = MH\).

Có \(SA \bot \left( {ABC} \right)\) nên \(SA \bot MI\), mà \(MI \bot AB,AB \cap SA = A\) nên \(MI \bot \left( {SAB} \right)\). Do đó \(IA = IB = IH\).

Hoàn toàn tương tự, ta cũng chỉ ra được \(IA = IC = IK\).

Do đó \(I\) là tâm mặt cầu ngoại tiếp của hình chóp \(A.BCHK\).

Bán kính của mặt cầu này là \(AI = \frac{{a\sqrt 3 }}{3}\) (do tam giác \(ABC\) đều cạnh \(a\)).