Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau

Trong không gian \(Oxyz\), cho các điểm \(A\left( { - 2;1;1} \right),B\left( {0;1; - 2} \right),C\left( {m;3 - 2m;1} \right)\).
Với \(\forall m \in \mathbb{R}\), trọng tâm có cao độ bằng ______.
Với \(m = \) ______ thì vuông tại \(A\).
Có ______ giá trị của tham số \(m\) để \({S_{ABC}} = 7\).

Trong không gian \(Oxyz\), cho các điểm \(A\left( { - 2;1;1} \right),B\left( {0;1; - 2} \right),C\left( {m;3 - 2m;1} \right)\).
Với \(\forall m \in \mathbb{R}\), trọng tâm có cao độ bằng ______.
Với \(m = \) ______ thì vuông tại \(A\).
Có ______ giá trị của tham số \(m\) để \({S_{ABC}} = 7\).
Quảng cáo
Trả lời:
Đáp án
Với \(\forall m \in \mathbb{R}\), trọng tâm có cao độ bằng 0.
Với \(m = \) -2 thì vuông tại \(A\).
Có 2 giá trị của tham số \(m\) để \({S_{ABC}} = 7\).
Giải thích
Với \(\forall m \in \mathbb{R}\), trọng tâm có cao độ bằng 0 .
Ta có:
\(\overrightarrow {AB} = \left( {2;0; - 3} \right);\overrightarrow {AC} = \left( {m + 2;2 - 2m;0} \right) \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = \left( {6m - 12; - 3m - 6;4 - 4m} \right)\)
Để vuông tại \(A\) thì \(AB \bot AC \Leftrightarrow 2\left( {m + 2} \right) + 0\left( {2 - 2m} \right) - 3.0 = 0 \Leftrightarrow m = - 2\).
\({S_{ABC}} = 7 \Leftrightarrow \frac{1}{2}\left| {\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right]} \right| = 7 \Leftrightarrow {(6m - 12)^2} + {( - 3m - 6)^2} + {(4 - 4m)^2} = {14^2}\)
\( \Leftrightarrow 61{m^2} - 140m = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 0}\\{m = \frac{{140}}{{61}}}\end{array}} \right.\).
Vậy có 2 giá trị của tham số \(m\) để \({S_{ABC}} = 7\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: “14”
Giải thích
Xét hàm số \(g\left( x \right) = f\left( {x - m} \right) - \frac{1}{2}{(x - m - 1)^2} + 2023\).
\(g'\left( x \right) = f'\left( {x - m} \right) - \left( {x - m - 1} \right)\). Xét phương trình \(g'\left( x \right) = 0{\rm{\;}}\) (1).
Đặt \(x - m = t\), phương trình (1) trở thành \(f'\left( t \right) - \left( {t - 1} \right) = 0 \Leftrightarrow f'\left( t \right) = t - 1{\rm{\;}}\) (2).
Nghiệm của phương trình \(\left( 2 \right)\) là hoành độ giao điểm của hai đồ thị \(y = f'\left( t \right)\) và \(y = t - 1\).
Ta có đồ thị các hàm số \(y = f'\left( t \right)\) và \(y = t - 1\) như sau:
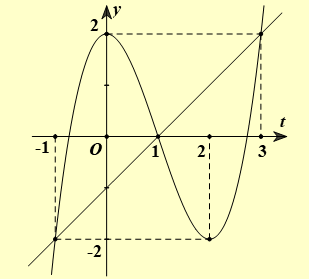
Căn cứ đồ thị các hàm số thì phương trình \(\left( 2 \right)\) có nghiệm là \(\left[ {\begin{array}{*{20}{c}}{t = - 1}\\{t = 1}\\{t = 3}\end{array} \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = m - 1}\\{x = m + 1}\\{x = m + 3}\end{array}} \right.} \right.\)
Ta có bảng biến thiên của \(y = g\left( x \right)\) như sau:
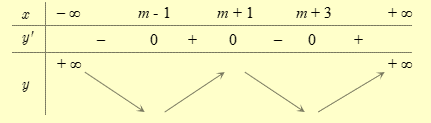
Để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {5;6} \right)\) thì \(\left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{m - 1 \le 5}\\{m + 1 \ge 6}\end{array}} \right.}\\{m + 3 \le 5}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{5 \le m \le 6}\\{m \le 2}\end{array}} \right.\)
Vì \(m \in \mathbb{N}{\rm{*}} \Rightarrow m \in \left\{ {1;2;5;6} \right\} \Rightarrow S = 14\).
Lời giải
Đáp án
Một cửa hàng điện máy có doanh số bán lẻ tivi mỗi năm là 2500 chiếc. Chi phí lưu kho của mỗi chiếc tivi là 200 nghìn đồng một năm. Để đặt hàng nhà sản xuất, mỗi lần cửa hàng cần đặt cọc cố định là 10 triệu đồng và sau khi nhập hàng thì cần trả thêm 3 triệu đồng mỗi chiếc tivi. Biết rằng số lượng tivi trung bình gửi trong kho bằng một nửa số tivi của mỗi lần đặt hàng. Cửa hàng nên đặt hàng nhà sản xuất (1) ___5___ lần mỗi năm và mỗi lần đặt (2) __500__ chiếc tivi để chi phí hàng tồn kho là thấp nhất.
Giải thích
Gọi \(x\) là số tivi mỗi lần đặt hàng \(\left( {x \in \mathbb{N},x \in \left[ {1;2500} \right]} \right)\).
Khi đó, số lượng tivi trung bình gửi trong kho sẽ là \(\frac{x}{2}\). Do đó, chi phí gửi hàng trong kho mỗi năm sẽ là \(0,2.\frac{x}{2} = \frac{x}{{10}}\).
Số lần đặt hàng mỗi năm sẽ là \(\frac{{2500}}{x}\).
Do đó chi phí đặt hàng mỗi năm sẽ là \(\left( {10 + 3x} \right).\frac{{2500}}{x} = \frac{{25000}}{x} + 7500\).
Suy ra, chi phí hàng tồn kho là \(C\left( x \right) = \frac{x}{{10}} + \frac{{25000}}{x} + 7500\).
Bài toán trở thành tìm giá trị nhỏ nhất của \(C\left( x \right)\) với \(x \in \left[ {1;2500} \right]\).
Ta có: \(C'\left( x \right) = \frac{1}{{10}} - \frac{{25000}}{{{x^2}}},C'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 500}\\{x = - 500\left( L \right)}\end{array}} \right.\)
Bảng biến thiên:
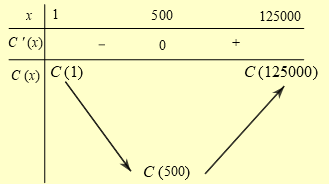
Vậy \(\mathop {{\rm{min}}}\limits_{\left[ {1;2500} \right]} C\left( x \right) = C\left( {500} \right) = 7600\)
Khi đó số lần đặt hàng mỗi năm sẽ là \(\frac{{2500}}{{500}} = 5\) lần.
Vậy để chi phí hàng tồn kho là nhỏ nhất thì cửa hàng cần đặt hàng 5 lần mỗi năm và 500 cái mỗi lần.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Diện tích mặt tròn xoay tạo thành khi quay đường cong \(f\left( x \right)\) quanh trục hoành giới hạn giữa hai mặt phẳng \(x = a,x = b\) được tính bởi công thức \(S = 2\pi \int\limits_a^b {\left| {f\left( x \right)} \right|\sqrt {1 + {{\left[ {f'\left( x \right)} \right]}^2}} {\rm{\;d}}x} \). Một bình hoa có dạng hình cầu khuyết như hình vẽ. Biết đường kính của bình hoa là \(20{\rm{\;cm}}\) và đường kính đáy/miệng của bình hoa là \(12{\rm{\;cm}}\). Diện tích tráng men mặt ngoài (kể cả đáy) của bình hoa bằng (1) _________ \(c{m^2}\). (Kết quả làm tròn đến chữ số thập phân thứ hai) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/11/blobid9-1731382856.png)