Cho hình “viên phân” (phần màu xanh) được giới hạn bởi dây cung có độ dài \[55{\rm{\;cm}}\] và cung có số đo \[95^\circ \] (hình vẽ).
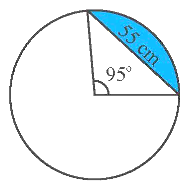
Diện tích hình viên phân đó (làm tròn kết quả đến hàng phần trăm) là
A. \[680,65{\rm{\;c}}{{\rm{m}}^2}.\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
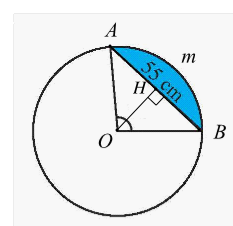
Kẻ \[OH \bot AB\] tại \[H.\]
Tam giác \[OAB\] cân tại \[O\] (do \[OA = OB = R\]) có \[OH\] là đường cao, suy ra \[OH\] cũng là đường trung tuyến của tam giác. Do đó \[H\] là trung điểm \[AB.\]
Vì vậy \[HB = \frac{{AB}}{2} = \frac{{55}}{2} = {\rm{27,5\;(cm)}}{\rm{.}}\]
Tam giác \[OAB\] cân tại \[O\] có \[OH\] là đường cao, suy ra \[OH\] cũng là đường phân giác của tam giác.
Do đó \[\widehat {BOH} = \frac{{\widehat {AOB}}}{2} = \frac{{95^\circ }}{2} = 47,5^\circ .\]
Vì tam giác \[OBH\] vuông tại \[H\] nên:
⦁ \[\sin \widehat {BOH} = \frac{{HB}}{{OB}},\] suy ra \[OB = \frac{{HB}}{{\sin \widehat {BOH}}} = \frac{{27,5}}{{\sin 47,5^\circ }}{\rm{\;(cm);}}\]
⦁ \[\tan \widehat {BOH} = \frac{{HB}}{{OH}},\] suy ra \[OH = \frac{{HB}}{{\tan \widehat {BOH}}} = \frac{{27,5}}{{\tan 47,5^\circ }}{\rm{\;(cm)}}{\rm{.}}\]
Diện tích tam giác \[OAB\] là:
\[{S_{\Delta OAB}} = \frac{1}{2} \cdot OH \cdot AB = \frac{1}{2} \cdot \frac{{27,5}}{{\tan 47,5^\circ }} \cdot 55 = \frac{{3025}}{{4 \cdot \tan 47,5^\circ }} \approx 692,98{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Diện tích hình quạt tròn \[AOB\] là:
\[{S_{hqAOB}} = \frac{n}{{360}} \cdot \pi {R^2} = \frac{{95}}{{360}} \cdot \pi \cdot O{B^2} = \frac{{19}}{{72}} \cdot \pi \cdot {\left( {\frac{{27,5}}{{\sin 47,5^\circ }}} \right)^2} \approx 1\,\,153,39{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Khi đó, diện tích hình viên phân cần tìm là:
\[S = {S_{hqAOB}} - {S_{\Delta OAB}} \approx 1\,\,153,39 - 692,98 = 460,41{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Vậy ta chọn phương án B.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[25\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
Vì \[OA = OM = 10{\rm{\;(cm)}}\] nên tam giác \[OAM\] cân tại \[O.\]
Mà \[\widehat {BAM} = 45^\circ \], suy ra tam giác \[OAM\] vuông cân tại \[O.\]
Do đó số đo cung nhỏ \[AM\] là:
Diện tích hình quạt \[AOM\] là: \[S = \frac{n}{{360}}\pi {R^2} = \frac{{90}}{{360}}\pi \cdot {10^2} = 25\pi {\rm{\;(c}}{{\rm{m}}^2}).\]
Vậy diện tích hình quạt \[AOM\] bằng \[25\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Do đó ta chọn phương án A.
Câu 2
A. \[\frac{{4\sqrt 2 }}{3}\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: C
Ta có \[OB = OC\] nên tam giác \[OBC\] cân tại \[O.\] Suy ra \[\widehat {OCB} = \widehat {OBC} = 30^\circ .\]
Tam giác \[OBC\] có: \[\widehat {BOC} + \widehat {OCB} + \widehat {OBC} = 180^\circ \] (định lí tổng ba góc của một tam giác)
Suy ra \[\widehat {BOC} = 180^\circ - \left( {\widehat {OCB} + \widehat {OBC}} \right) = 180^\circ - \left( {30^\circ + 30^\circ } \right) = 120^\circ .\]
Do đó
Bán kính đường tròn \[\left( O \right)\] là: \[R = \frac{{AB}}{2} = \frac{{2\sqrt 2 }}{2} = \sqrt 2 {\rm{\;(cm)}}{\rm{.}}\]
Diện tích hình quạt \[BAC\] là: \[{S_q} = \frac{n}{{360}} \cdot \pi {R^2} = \frac{{240}}{{360}} \cdot \pi \cdot {\left( {\sqrt 2 } \right)^2} = \frac{{4\pi }}{3}{\rm{\;(c}}{{\rm{m}}^2}).\]
Vậy diện tích hình quạt \[BAC\] bằng \[\frac{{4\pi }}{3}{\rm{\;c}}{{\rm{m}}^2}.\]
Do đó ta chọn phương án C.
Câu 3
A. \[85^\circ .\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[\frac{1}{n}.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[\frac{{4\pi }}{3}{\rm{\;dm}}.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Hình quạt tròn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[234\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập