III. Vận dụng
Cho đường tròn \[\left( {A;10{\rm{\;cm}}} \right),\,\,\left( {B;15{\rm{\;cm}}} \right),\,\,\left( {C;15{\rm{\;cm}}} \right)\] tiếp xúc ngoài với nhau đôi một. Hai đường tròn \[\left( B \right)\] và \[\left( C \right)\] tiếp xúc nhau tại \[A'.\] Đường tròn \[\left( A \right)\] tiếp xúc với đường tròn \[\left( B \right)\] và \[\left( C \right)\] lần lượt tại \[C',B'.\] Cho các nhận định sau:
(i) \[AA'\] là tiếp tuyến chung của hai đường tròn \[\left( B \right)\] và \[\left( C \right).\]
(ii) \[AA' = 15{\rm{\;cm}}.\]
Khẳng định nào sau đây là đúng nhất?
A. Chỉ có (i) đúng.
B. Chỉ có (ii) đúng.
C. Cả (i) và (ii) đều đúng.
D. Cả (i) và (ii) đều sai.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
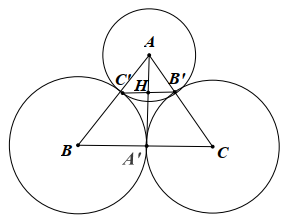
Ta có:
⦁ \[AB = AC' + C'B = 10 + 15 = 25{\rm{\;(cm)}};\]
⦁ \[AC = AB' + B'C = 10 + 15 = 25{\rm{\;(cm)}};\]
⦁ \[BC = BA' + A'C = 15 + 15 = 30{\rm{\;(cm)}}{\rm{.}}\]
Suy ra tam giác \[ABC\] cân tại \[A.\]
Vì \[BA' = A'C = 15{\rm{\;(cm)}}\] nên \[A'\] là trung điểm \[BC.\]
Tam giác \[ABC\] cân tại \[A\] có \[AA'\] là đường trung tuyến nên \[AA'\] cũng là đường cao của tam giác \[ABC\] hay \[AA' \bot BC\] tại \[A'\] thuộc cả hai đường tròn \[\left( {B;15{\rm{\;cm}}} \right),\,\,\left( {C;15{\rm{\;cm}}} \right).\]
Vì vậy \[AA'\] là tiếp tuyến chung của hai đường tròn \[\left( {B;15{\rm{\;cm}}} \right),\,\,\left( {C;15{\rm{\;cm}}} \right).\]
Áp dụng định lí Pythagore cho tam giác \[AA'B\] vuông tại \[A',\] ta được: \[A{B^2} = A{A'^2} + B{A'^2}.\]
Suy ra \[A{A'^2} = A{B^2} - B{A'^2} = {25^2} - {15^2} = 400.\] Do đó \[AA' = 20{\rm{\;(cm)}}{\rm{.}}\]
Do đó chỉ có nhận định (i) là đúng. Vậy ta chọn phương án A.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. tam giác tù.
B. tam giác cân.
C. tam giác vuông.
D. tam giác vuông cân.
Lời giải
Đáp án đúng là: C
Vì \[{O_1}A = {O_1}B\] nên tam giác \[{O_1}AB\] cân tại \[{O_1}.\] Do đó \[\widehat {{O_1}AB} = \widehat {{O_1}BA}.\]
Chứng minh tương tự, ta được \[\widehat {{O_2}AC} = \widehat {{O_2}CA}.\]
Ta có đường thẳng \[\left( d \right)\] tiếp xúc với \[\left( {{O_1}} \right),\left( {{O_2}} \right)\] lần lượt tại \[B,C\] nên \[{O_1}B \bot BC\] tại \[B\] và \({O_2}C \bot BC\) tại \(C.\)
Xét tứ giác \({O_1}BC{O_2}\) ta có: \[\widehat {{O_1}} + \widehat {{O_2}} = 360^\circ - \widehat {B\,} - \widehat {C\,} = 360^\circ - 90^\circ - 90^\circ = 180^\circ \]
Suy ra \[\left( {180^\circ - \widehat {{O_1}AB} - \widehat {{O_1}BA}} \right) + \left( {180^\circ - \widehat {{O_2}AC} - \widehat {{O_2}CA}} \right) = 180^\circ \]
Khi đó \[2 \cdot \widehat {{O_1}AB} + 2 \cdot \widehat {{O_2}AC} = 180^\circ \]
Vì vậy \[2 \cdot \left( {\widehat {{O_1}AB} + \widehat {{O_2}AC}} \right) = 180^\circ \]
Suy ra \[\widehat {{O_1}AB} + \widehat {{O_2}AC} = 90^\circ \]
Ta có \[\widehat {{O_1}AB} + \widehat {BAC} + \widehat {{O_2}AC} = 180^\circ \]
Suy ra \[\widehat {BAC} = 180^\circ - \left( {\widehat {{O_1}AB} + \widehat {{O_2}AC}} \right) = 180^\circ - 90^\circ = 90^\circ .\]
Vậy tam giác \[ABC\] vuông tại \[A.\]
Do đó ta chọn phương án C.
Câu 2
A. \[BC = 2R.\]
B. \[BC = R\sqrt 2 .\]
C. \[BC = R\sqrt 3 .\]
D. \[BC = R\sqrt 6 .\]
Lời giải
Đáp án đúng là: B
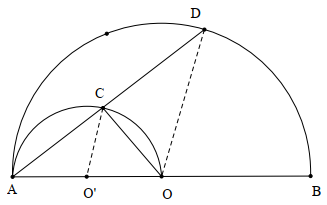
Vì đường tròn tâm \(O'\) có \[AO\] là đường kính nên \(O'C = O'O = \frac{{AO}}{2} = \frac{R}{2}.\)
Ta có \[OB = R\] và \[O'B = OO' + OB = \frac{R}{2} + R = \frac{{3R}}{2}.\]
Vì \[BC\] là tiếp tuyến của nửa đường tròn \[\left( {O'} \right)\] nên \[O'C \bot BC\] tại \[C.\]
Áp dụng định lí Pythagore cho tam giác \[O'BC\] vuông tại \[C,\] ta được \[O'{B^2} = O'{C^2} + B{C^2}.\]
Suy ra \[B{C^2} = O'{B^2} - O'{C^2} = {\left( {\frac{{3R}}{2}} \right)^2} - {\left( {\frac{R}{2}} \right)^2} = 2{R^2}.\]
Do đó \[BC = R\sqrt 2 .\]
Vậy ta chọn phương án B.
Câu 3
A. \(1{\rm{\;cm}}{\rm{.}}\)
B. \(2{\rm{\;cm}}.\)
C. \(4{\rm{\;cm}}.\)
D. \(8{\rm{\;cm}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[\Delta ABC = \Delta DBC.\]
B. \[BD \bot CD.\]
C. \[CD\] là tiếp tuyến của \[\left( {B;BA} \right).\]
D. Cả A, B, C đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[12{\rm{\;c}}{{\rm{m}}^2}.\]
B. \[24{\rm{\;c}}{{\rm{m}}^2}.\]
C. \[12\sqrt 3 {\rm{\;c}}{{\rm{m}}^2}.\]
D. \[16{\rm{\;c}}{{\rm{m}}^2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(1{\rm{\;cm}}{\rm{.}}\)
B. \(2{\rm{\;cm}}.\)
C. \(6{\rm{\;cm}}.\)
D. \({\rm{12\;cm}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';r} \right)\] ở ngoài nhau.
B. đường tròn \[\left( {O;R} \right)\] đựng \[\left( {O';r} \right).\]
C. đường tròn \[\left( {O';r} \right)\] và \[\left( {O;R} \right).\]
D. hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O';r} \right)\] cắt nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo