Cho tam giác \[ABC\] vuông tại \[A\] đường cao \[AH\]. Kẻ \[HE\] vuông góc với \[AB\] tại \[E\], kẻ \[HF\] vuông góc với \[AC\] tại \[F\]. Chọn câu đúng:
A. Tứ giác \[BEFC\] là tứ giác nội tiếp.
B. Tứ giác \[BEFC\] không nội tiếp.
C. Tứ giác \[AFHE\] là hình vuông.
D. Tứ giác \[AFHE\] không nội tiếp.
Quảng cáo
Trả lời:
Đáp án đúng là: A
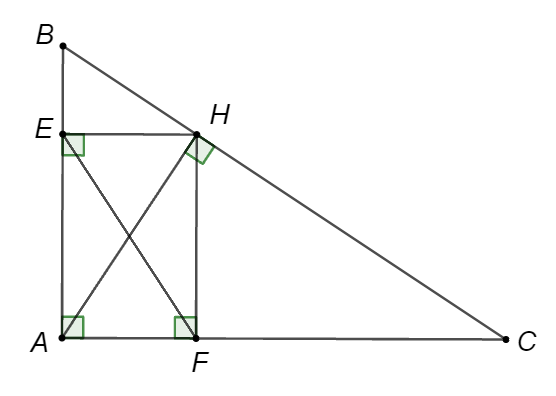
Xét tứ giác \[AEHF\] có: \(\widehat A = \widehat E = \widehat F = 90^\circ \)
Suy ra tứ giác \[AEHF\] là hình chứ nhật.
Suy ra tứ giác \[AEHF\] là tứ giác nội tiếp (có tổng hai góc đối diện bằng \(180^\circ \)).
Do đó \(\widehat {AFE} = \widehat {AHE}\) (hai góc nội tiếp cùng chắn cung \[AE\])
Mà \(\widehat {AHE} = \widehat {ABH}\) (cùng phụ góc \[BHE\])
Suy ra \(\widehat {AFE} = \widehat {ABC}\).
Xét tứ giác \[BEFC\] có: \(\widehat {AFE} = \widehat {ABC}\)
Góc \[AFE\] là góc ngoài tại đỉnh \[F\].
Suy ra \[BEFC\] là tứ giác nội tiếp.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Tứ giác \[PMAC\] là tứ giác nội tiếp.
B. Tam giác \[BCM\] vuông.
C. Tam giác \[BCP\] có \[CM\] là đường trung tuyến.
D. Không có khẳng định nào đúng.
Lời giải
Đáp án đúng là: A
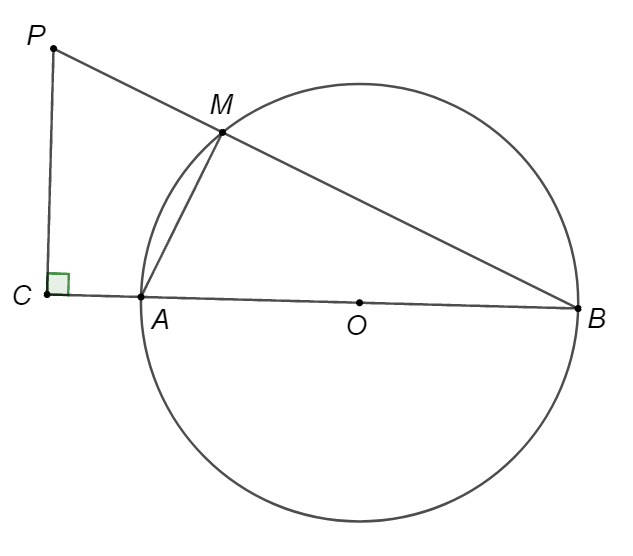
Ta có \(\widehat {AMB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Lại có: \(BC \bot CP\) hay \(\widehat {BCP} = 90^\circ \).
Suy ra \(\widehat {AMB} + \widehat {BCP} = 180^\circ \).
Nên \[\widehat {PMA} + \widehat {PCA} = 180^\circ \].
Do đó tứ giác \[PMAC\] là tứ giác nội tiếp.
Câu 2
A. \(80^\circ \).
B. \(90^\circ \).
C. \(100^\circ \).
D. \(110^\circ \).
Lời giải
Đáp án đúng là: C
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh)
Đặt \(\widehat {BCE} = \widehat {DCF} = x\).
Theo tính chất góc ngoài tam giác, ta có:
\(\widehat {ABC} = \widehat {BCE} + \widehat E = x + 40^\circ \)
\(\widehat {ADC} = \widehat {DCF} + \widehat F = x + 20^\circ \)
Lại có \(\widehat {ABC} + \widehat {ADC} = 180^\circ \) (hai góc đối diện của tứ giác nội tiếp)
Suy ra \(\left( {x + 40^\circ } \right) + \left( {x + 20^\circ } \right) = 180^\circ \) hay \(x = 60^\circ \).
Do đó \(\widehat {ABC} = 60^\circ + 40^\circ = 100^\circ \).
Câu 3
A. Tứ giác \[ABOC\]là hình thoi.
B. Tứ giác \[ABOC\] nội tiếp.
C. Tứ giác \[ABOC\] không nội tiếp.
D. Tứ giác \[ABOC\] là hình bình hành.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(110^\circ \).
B. \(30^\circ \).
C. \(70^\circ \).
D. \(55^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. cân tại \[F\].
B. cân tại \[C\].
C. cân tại \[A\].
D. đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
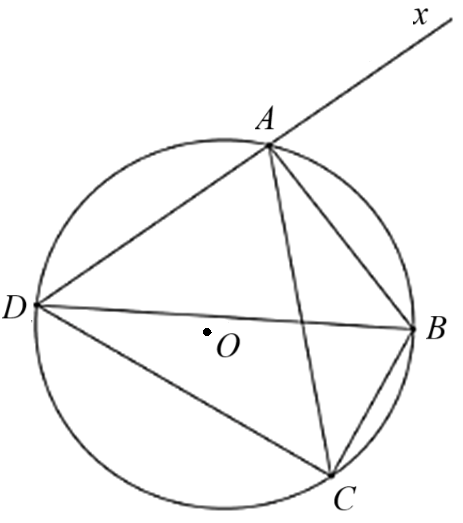
Câu 6
A. \(\widehat {BDC} = \widehat {BAC}\).
B. \(\widehat {BAC} = \widehat {BAx}\).
C. \(\widehat {DCB} = \widehat {BAx}.\)
D. \(\widehat {ABC} + \widehat {ADC} = 180^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hình vẽ dưới đây:Số đo góc \[ABC\] là (ảnh 1)](https://video.vietjack.com/upload2/images/1731491184/1731491902-image10.png)