Câu hỏi:
14/11/2024 737Cho bát giác đều \[ABCDEFGH\] có tâm \[O.\] Phép quay thuận chiều \[135^\circ \] tâm \[O\] biến điểm \[D\] của bát giác đều \[ABCDEFGH\] thành điểm nào?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
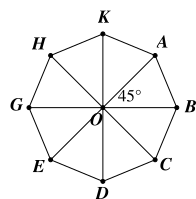
Giả sử \[ABCDEGHK\] là bát giác đều có tâm \[O.\]
Do đó \[AB = BC = CD = DE = EG = GH = HK\] và \[OA = OB = OC = OD = OE = OG = OH = OK.\]
Xét \[\Delta OAB\] và \[\Delta OBC\] có: \[OA = OB,{\rm{ }}OB = OC,{\rm{ }}AB = BC\].
Do đó \[\Delta OAB = \Delta OBC\,\,\left( {{\rm{c}}{\rm{.c}}{\rm{.c}}} \right)\].
Tương tự, ta sẽ chứng minh được:
\[\Delta OAB = \Delta OBC = \Delta COD = \Delta DOE = \Delta EOG = \Delta GOH = \Delta HOK = \Delta KOA.\]
Suy ra các góc tương ứng bằng nhau:
\(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOG} = \widehat {GOH} = \widehat {HOK} = \widehat {KOA}.\)
Ta có: \(\widehat {AOB} + \widehat {BOC} + \widehat {COD} + \widehat {DOE} + \widehat {EOG} + \widehat {GOH} + \widehat {HOK} + \widehat {KOA} = 360^\circ \)
Suy ra \(8\widehat {AOB} = 360^\circ ,\) nên \(\widehat {AOB} = 45^\circ .\)
Do đó, \(\widehat {DOE} = \widehat {EOG} = \widehat {GOH} = 45^\circ .\)
Như vậy, ta sẽ có \[\widehat {DOG} = \widehat {DOE} + \widehat {EOF} + \widehat {FOG} = 45^\circ + 45^\circ + 45^\circ = 135^\circ .\]
Vậy quay thuận chiều \[135^\circ \] tâm \[O\] biến điểm \[D\] của bát giác đều \[ABCDEFGH\] thành điểm \[G.\]
Do đó ta chọn phương án A.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
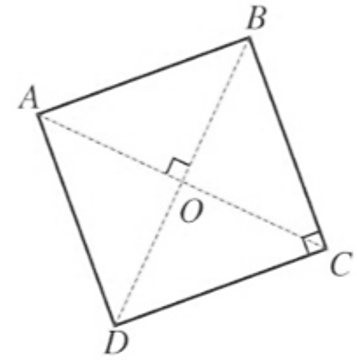
Cho hình vuông \[ABCD\] tâm \[O.\] Phép quay ngược chiều 180° tâm O biến các điểm \[A,\,\,B,\,\,C,\,\,D\] thành các điểm nào?
Xem đáp án »
14/11/2024
3,151
Câu 2:
Cho đa giác đều 9 cạnh có tâm \[O\] và \[AB,{\rm{ }}BC\] là hai cạnh của đa giác (như hình vẽ).
Số đo các góc \[\widehat {AOB}\,,\,\,\widehat {ABO}\,,\,\,\widehat {ABC}\] lần lượt là
Xem đáp án »
14/11/2024
3,111
Câu 3:
Cho hình ngũ giác đều \[ABCDE\] tâm \[O\]. Các phép quay tâm \[O\] giữ nguyên hình ngũ giác đều là
Xem đáp án »
14/11/2024
2,127
Câu 4:
Cho ngũ giác đều \[MNPQR\] có tâm \[O.\] Phép quay nào với tâm \[O\] biến ngũ giác đều \[MNPQR\] thành chính nó?
Xem đáp án »
14/11/2024
1,009
Câu 5:
Phép quay với \[O\] là tâm biến tam giác đều thành chính nó là phép quay thuận chiều một góc
Xem đáp án »
14/11/2024
991
Câu 6:
III. Vận dụng
Cho lục giác đều \[ABCDEF\] tâm \[O.\] Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của \[EF,{\rm{ }}BD.\] Khẳng định nào sau đây là sai?
Xem đáp án »
14/11/2024
301
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận