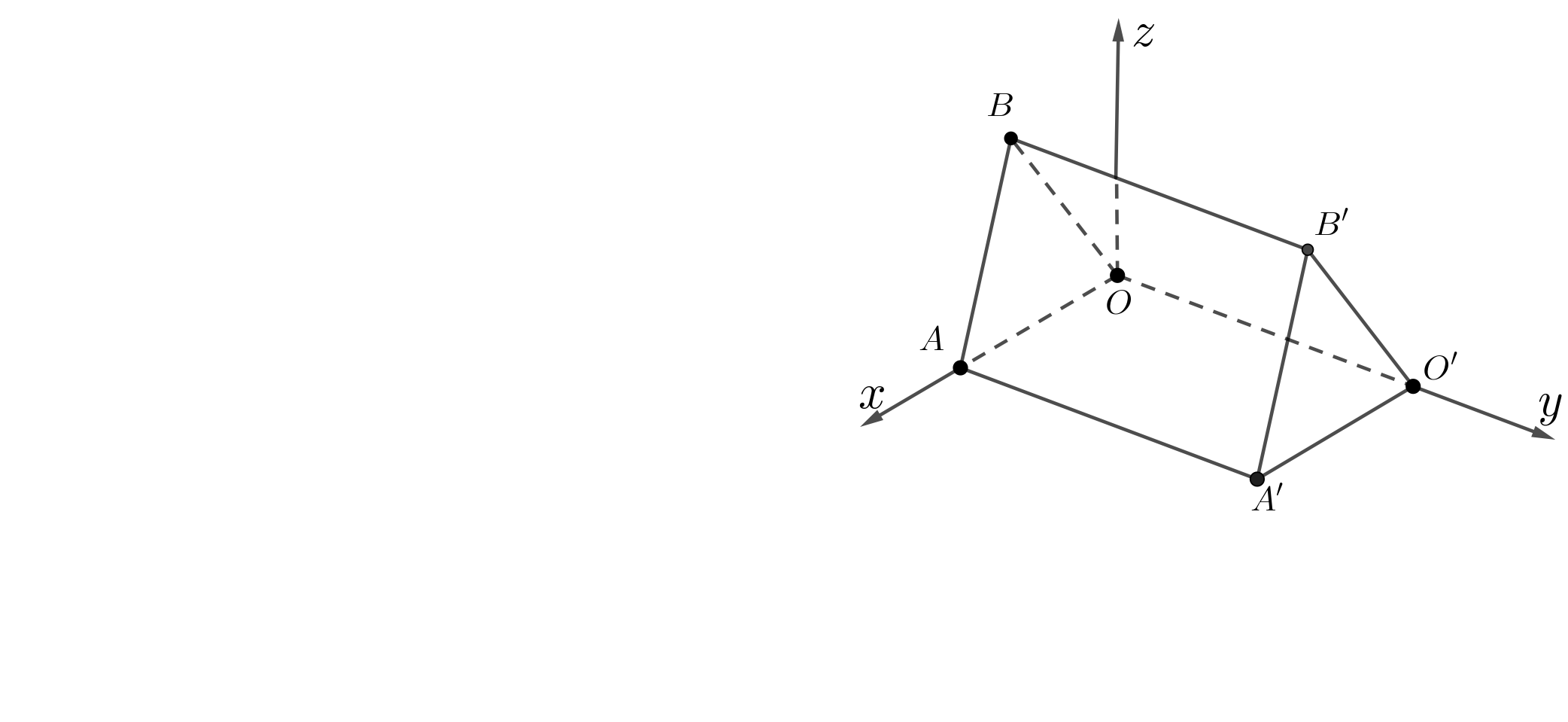
Trong không gian với hệ trục tọa độ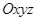 
, cho 
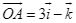với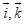 
là hai vectơ đơn vị trên hai trục tọa độ 
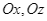, hai điểm 
.
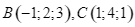a)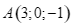 
.
b) Ba điểm 
thẳng hàng.
c) Điểm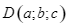 
là điểm đối xứng với 
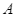qua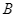 
. Khi đó 
.
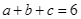d) Điểm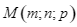 
trên mặt phẳng 
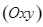sao cho 
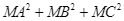đạt giá trị nhỏ nhất. Khi đó 
.
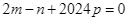Trong không gian với hệ trục tọa độ , cho với là hai vectơ đơn vị trên hai trục tọa độ , hai điểm .
a) .
b) Ba điểm thẳng hàng.
c) Điểm là điểm đối xứng với qua . Khi đó .
d) Điểm trên mặt phẳng sao cho đạt giá trị nhỏ nhất. Khi đó .
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 12 Cánh Diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đ, b) S, c) Đ, d) Đ
a) Vì 
.
b) Ta có 
.
Do 
không cùng phương nên suy ra 
không thẳng hàng.
c) Điểm 
là điểm đối xứng với 
qua 
nên là trung điểm của 
.
Ta có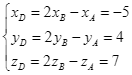 
. Suy ra 
.
Suy ra 
. Vậy 
.
d) Gọi 
là điểm thỏa mãn 
.
Ta có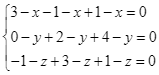 
.
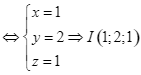Ta có 
.
Do 
không thay đổi nên nhỏ nhất khi 
nhỏ nhất hay 
là hình chiếu của điểm 
trên mặt phẳng 
.
Do đó 
. Suy ra 
. Vậy 
.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: 1013
Vì điểm 
có toạ độ là 
nên khoảng cách từ đến các trục 
lần lượt là 
và 
. Suy ra 
và 
.
Từ giả thiết suy ra 
,
do đó 
.
Vì 
và 
nằm trên trục 
nên toạ độ của điểm là 
.
Do đó 
và 
.
Vậy mỗi căn lều gỗ có chiều dài là , chiều rộng là , mỗi cạnh bên của mặt tiền có độ dài là 323 cm.
.
Lời giải
Trả lời: 52
Xét hàm số:
.
.
TXĐ: 
.
Ta có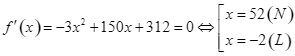 
.
Bảng biến thiên:
Hàm số đạt giá trị cực đại 
tại 
.
Vậy lợi nhuận của công ty đạt cực đại khi số sản phẩm .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo