Giải bài toán sau bằng cách lập hệ phương trình:
Lớp 9A và lớp 9B có tổng cộng 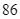 học sinh. Trong đợt thu nhặt giấy báo cũ thực hiện kế hoạch nhỏ, mỗi lớp có 3 bạn góp được
học sinh. Trong đợt thu nhặt giấy báo cũ thực hiện kế hoạch nhỏ, mỗi lớp có 3 bạn góp được 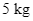 , các bạn còn lại mỗi bạn góp
, các bạn còn lại mỗi bạn góp  . Tính số học sinh của mỗi lớp, biết lớp 9B góp nhiều hơn lớp 9A là
. Tính số học sinh của mỗi lớp, biết lớp 9B góp nhiều hơn lớp 9A là 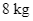 giấy báo cũ.
giấy báo cũ.
Lớp 9A và lớp 9B có tổng cộng ![]() học sinh. Trong đợt thu nhặt giấy báo cũ thực hiện kế hoạch nhỏ, mỗi lớp có 3 bạn góp được
học sinh. Trong đợt thu nhặt giấy báo cũ thực hiện kế hoạch nhỏ, mỗi lớp có 3 bạn góp được ![]() , các bạn còn lại mỗi bạn góp
, các bạn còn lại mỗi bạn góp ![]() . Tính số học sinh của mỗi lớp, biết lớp 9B góp nhiều hơn lớp 9A là
. Tính số học sinh của mỗi lớp, biết lớp 9B góp nhiều hơn lớp 9A là ![]() giấy báo cũ.
giấy báo cũ.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Gọi ![]() là số học sinh của lớp 9A,
là số học sinh của lớp 9A, ![]() là số học sinh của lớp 9B
là số học sinh của lớp 9B ![]() .
.
Theo đề bài, tổng số học sinh hai lớp là ![]() học sinh nên ta có phương trình
học sinh nên ta có phương trình ![]()
Lớp 9A góp được số giấy báo cũ là ![]() .
.
Lớp 9B góp được số giấy báo cũ là ![]() .
.
Mà lớp 9B góp nhiều hơn lớp 9A là ![]() giấy báo cũ nên ta có phương trình:
giấy báo cũ nên ta có phương trình:
![]() suy ra
suy ra ![]() hay
hay ![]() .
.
Từ (1) và (2) ta có hệ phương trình: 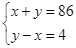 .
.
Cộng từng vế của hai phương trình trong hệ phương trình, ta được ![]() , suy ra
, suy ra ![]() (thỏa mãn).
(thỏa mãn).
Thay ![]() vào phương trình (1), ta được
vào phương trình (1), ta được ![]() , suy ra
, suy ra ![]() (thỏa mãn).
(thỏa mãn).
Vậy lớp 9A có ![]() học sinh, lớp 9B có
học sinh, lớp 9B có ![]() học sinh.
học sinh.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
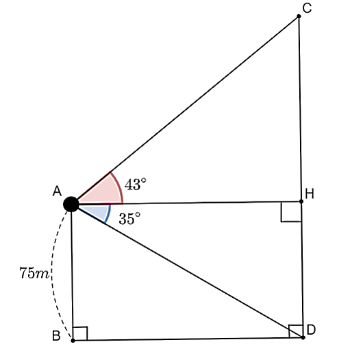
Ta có: ![]() nên tứ giác
nên tứ giác ![]() là hình chữ nhật.
là hình chữ nhật.
Do đó, ![]()
Xét tam giác ![]() vuông tại
vuông tại ![]() , có:
, có: ![]() suy ra
suy ra ![]()
Xét tam giác ![]() vuông tại
vuông tại ![]() , có:
, có: ![]()
Do đó, chiều cao ![]() là khoảng:
là khoảng: ![]()
Vậy chiều cao của trạm phát sóng đó khoảng ![]() .
.
Lời giải
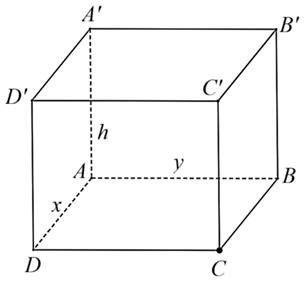
Theo đề bài, tỉ số giữa chiều cao \(h\) và chiều rộng đáy \(y\) bằng \(4\) nên \(h = 4y\).
Thể tích chiếc hộp \(3{\rm{ d}}{{\rm{m}}^3}\) nên \(xyh = 3{\rm{ }}\left( {{\rm{d}}{{\rm{m}}^3}} \right)\) hay \(4x{y^2} = 3\), suy ra \(x = \frac{3}{{4{y^2}}}\).
Do chiếc hộp không nắp, do đó diện tích bìa cần dùng là tổng diện tích đáy hộp và diện tích xung quanh của hộp.
Ta có: \(S = xy + 2h\left( {x + y} \right) = \frac{3}{{4{y^2}}} \cdot y + 2 \cdot 4y \cdot \left( {\frac{3}{{4{y^2}}} + y} \right)\)
\( = \frac{3}{{4y}} + \frac{6}{y} + 8{y^2} = \frac{{27}}{{4y}} + 8{y^2} = \frac{{27}}{{8y}} + \frac{{27}}{{8y}} + 8{y^2}\).
Do \(y\) là chiều rộng của hộp nên \(y > 0\).
Do đó, áp dụng bất đẳng thức Cauchy cho ba số \(\frac{{27}}{{8y}}\,;\,\,\frac{{27}}{{8y}}\,;\,\,8{y^2}\) không âm, ta được:
\(\frac{{27}}{{8y}} + \frac{{27}}{{8y}} + 8{y^2} \ge 3 \cdot \sqrt[3]{{\frac{{27}}{{8y}} \cdot \frac{{27}}{{8y}} \cdot 8{y^2}}}\), suy ra \(S \ge \frac{{27}}{2}.\)
Dấu “=” xảy ra khi và chỉ khi \(\frac{{27}}{{8y}} = 8{y^2}\), hay \({y^3} = \frac{{27}}{{64}}\) nên \(y = \frac{3}{4}\) (dm).
Do đó, \(x = \frac{3}{{4{y^2}}} = \frac{3}{{4 \cdot {{\left( {\frac{3}{4}} \right)}^2}}} = \frac{4}{3}{\rm{ }}\left( {{\rm{dm}}} \right)\).
Vậy lượng bìa cần dùng ít nhất có diện tích là \(\frac{{27}}{2}{\rm{ }}\left( {{\rm{d}}{{\rm{m}}^2}} \right)\) khi chiều dài \(x = \frac{4}{3}\) dm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

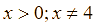
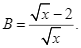
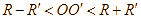 . Số điểm chung của hai đường tròn là
. Số điểm chung của hai đường tròn là