Câu hỏi:
11/12/2024 4,430
Một kĩ sư xây dựng đứng ở vị trí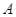 
(nóc của tòa nhà) dùng thiết bị để quan sát trạm thu phát sóng. Kĩ sư quan sát đỉnh 
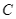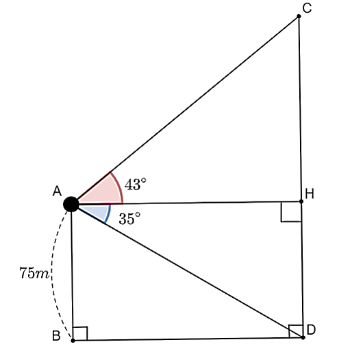
và chân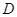 
của trạm thu phát sóng dưới hai góc nhìn (so với phương ngang) lần lượt là 
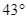và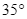 
. Biết chiều cao của tòa nhà là 
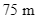, hãy tính chiều cao 
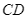của trạm phát sóng (kết quả làm tròn đến hàng phần trăm).
|
Một kĩ sư xây dựng đứng ở vị trí
|
|
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: 
nên tứ giác 
là hình chữ nhật.
Do đó, 
Xét tam giác 
vuông tại 
, có: 
suy ra 
Xét tam giác 
vuông tại , có: 
Do đó, chiều cao 
là khoảng: 
Vậy chiều cao của trạm phát sóng đó khoảng 
.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi 
là số học sinh của lớp 9A, 
là số học sinh của lớp 9B 
.
Theo đề bài, tổng số học sinh hai lớp là 
học sinh nên ta có phương trình 
Lớp 9A góp được số giấy báo cũ là 
.
Lớp 9B góp được số giấy báo cũ là 
.
Mà lớp 9B góp nhiều hơn lớp 9A là 
giấy báo cũ nên ta có phương trình:
suy ra 
hay 
.
Từ (1) và (2) ta có hệ phương trình: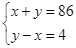 
.
Cộng từng vế của hai phương trình trong hệ phương trình, ta được 
, suy ra 
(thỏa mãn).
Thay vào phương trình (1), ta được 
, suy ra 
(thỏa mãn).
Vậy lớp 9A có 
học sinh, lớp 9B có 
học sinh.
Lời giải
Đáp án đúng là: C
Cách 1: Sử dụng MTCT để tìm nghiệm của hệ hai phương trình 
Với MTCT phù hợp, ta bấm lần lượt các phím:
Trên màn hình cho kết quả 
ta bấm tiếp phím 
màn hình cho kết quả 
Vậy cặp số 
là nghiệm của hệ phương trình
Cách 2: Xét hệ phương trình
Thực hiện cộng theo vế hai phương trình ta được 
, suy ra 
Thay 
vào phương trình thứ nhất ta được: 
hay 
, suy ra 
.
Vậy cặp số 
là nghiệm của hệ phương trình.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
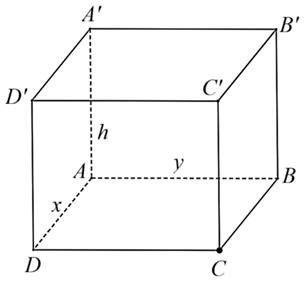
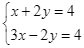
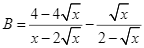
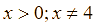
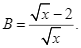
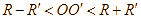. Số điểm chung của hai đường tròn làLời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1