Câu hỏi:
11/12/2024 5,769
Bác An có mảnh vườn hình vuông 
có cạnh bằng 
. Ở bốn góc vườn, bác An muốn trồng hoa vào các phần đất hình tam giác vuông bằng nhau (hình vẽ). Hãy tính khoảng cách từ góc vườn 
đến vị trí 
sao cho tứ giác 
có chu vi nhỏ nhất.
có cạnh bằng . Ở bốn góc vườn, bác An muốn trồng hoa vào các phần đất hình tam giác vuông bằng nhau (hình vẽ). Hãy tính khoảng cách từ góc vườn đến vị trí sao cho tứ giác có chu vi nhỏ nhất.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi độ dài của đoạn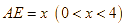 
(m), suy ra độ dài đoạn 
Theo đề, các phần đất hình tam giác bằng nhau, nên ta có:
và 
.
Áp dụng định lí Pythagore vào tam giác 
vuông tại 
, có:
Suy ra 
Do các phần hình tam giác bằng nhau nên 
.
Suy ra, chu vi 
là: 
.
Để chu vi của tứ giác nhỏ nhất thì 
nhỏ nhất.
Với mọi 
ta có:
.
Do đó, chu vi của tứ giác nhỏ nhất bằng 
khi 
hay 
Vậy khoảng cách từ đến 
bằng 
thì tứ giác có chu vi nhỏ nhất.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi 
(đồng) lần lượt là giá niêm yết của một thùng nước ngọt và một túi bánh sandwich (x > 0, y > 0).
Theo bài, cô Linh đi siêu thị mua 1 thùng nước ngọt và 4 túi bánh mì sandwich với giá niêm yết tổng cộng là 340 000 đồng nên ta có phương trình: 
(1)
Giá mỗi thùng nước ngọt sau khi tăng 
so với giá niêm yết là: 
(đồng).
Giá mỗi túi bánh mì sandwich được giảm 
so với giá niêm yết là:
(đồng).
Theo bài, khi thanh toán cô Linh chỉ cần trả tổng cộng 
đồng nên ta có phương trình: 
hay 
(2)
Từ (1) và (2) ta có hệ phương trình: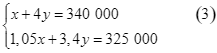 
Nhân cả hai vế của phương trình (1) với 
ta được hệ phương trình: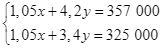 
Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ trên, ta được:
nên 
(thỏa mãn).
Thay 
vào phương trình (1), ta được:
nên 
(thỏa mãn).
Vậy một thùng nước ngọt và một túi bánh mì sandwich có giá niêm yết lần lượt là 
đồng và đồng.
Lời giải
Vẽ 
kéo dài tại 
và đường kính 
của đường tròn 
.
Ta có: 
(vì 
).
Để diện tích 
lớn nhất thì 
đạt giá trị lớn nhất, mà 
là đường kính đường tròn nên có giá trị không đổi, do đó ta cần 
đạt giá trị lớn nhất.
Mà 
(quan hệ giữa đường vuông góc và đường xiên)
Lại có, 
(trong một đường tròn, độ dài các dây cung luôn nhỏ hơn hoặc bằng đường kính).
Do đó, đạt giá trị lớn nhất khi 
hay 
, hay 
.
Suy ra 
thẳng hàng.
Vậy diện tích lớn nhất khi thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận