Để lập đội tuyển năng khiếu môn bóng rổ của trường, thầy thể dục đưa ra quy định tuyển chọn như sau: mỗi bạn dự tuyển sẽ được ném 15 quả bóng vào rổ, quả bóng vào rổ được cộng thêm 2 điểm; quả bóng ném ra ngoài bị trừ 1 điểm. Nếu bạn nào có số điểm từ 15 điểm trở lên thì sẽ được chọn vào đội tuyển.

Viết bất phương trình phù hợp với tình huống trên.

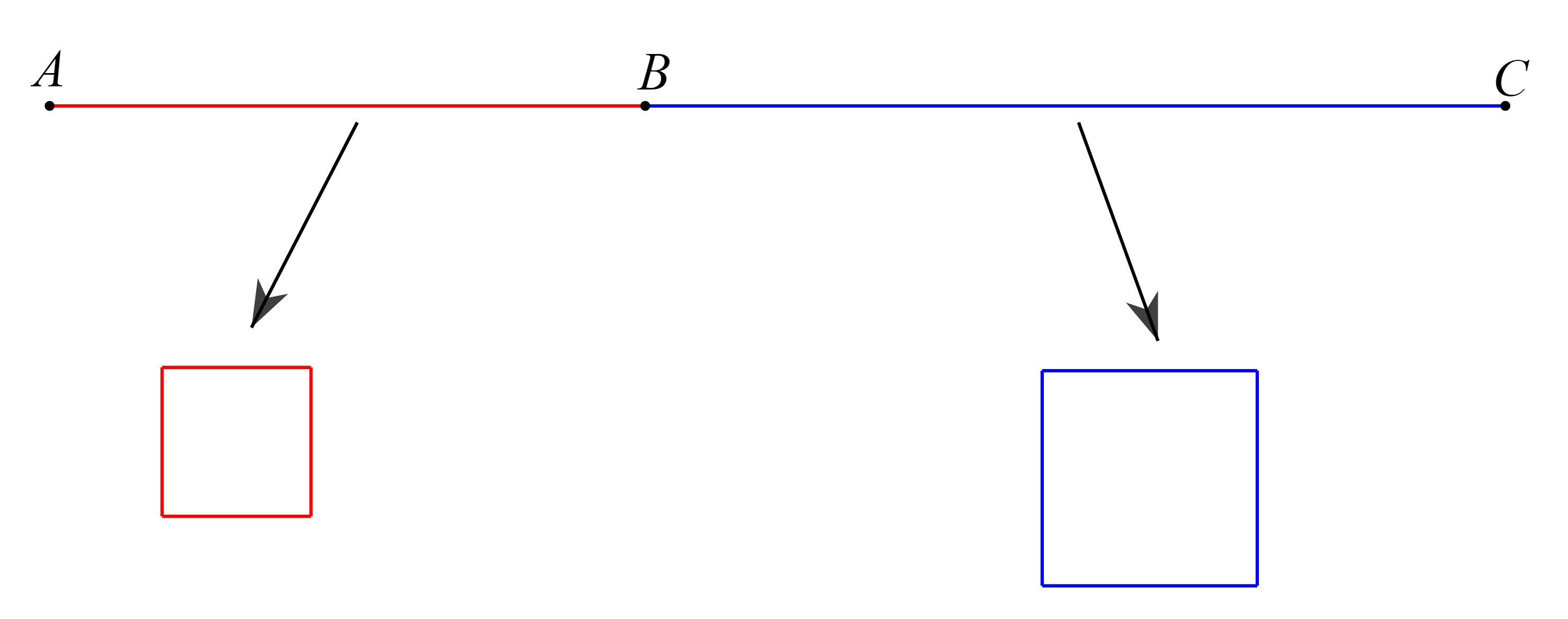
Gọi cạnh hình vuông được uốn từ đoạn là (

, đơn vị: m).

Lúc này, độ dài đoạn chính là chu vi hình vuông đó và bằng (m).

Do đó, độ dài đoạn là (m).

Suy ra, độ dài cạnh hình vuông được uốn bởi đoạn là (m).

Tổng diện tích hai hình vuông lúc này là:

Ta có: .

Tổng diện tích hai hình vuông đạt giá trị nhỏ nhất bằng khi hay

Khi đó, độ dài đoạn thẳng và độ dài đoạn thẳng hay là trung điểm của đoạn .

Vậy để tổng diện tích hai hình vuông đạt giá trị nhỏ nhất thì ta chia đoạn dây thép thành hai phần bằng nhau

Gọi là số sản phẩm đội phải làm theo kế hoạch (, đơn vị: sản phẩm) và là số ngày đội đó làm theo kế hoạch (, đơn vị: ngày).

Theo kế hoạch, số sản phẩm phải làm là: (1).

Thực tế, mỗi ngày đội làm được 60 sản phẩm và hoàn thành trước 2 ngày đồng thời làm thêm được 24 sản phẩm.

Do đó, dựa vào số sản phẩm thực tế, ta có phương trình: hay (2).

Từ (1) và (2) ta có hệ phương trình: .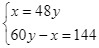

Thay vào phương trình (2), ta được:

, suy ra  nên (thỏa mãn).

Thay vào phương trình , được (thỏa mãn).

Vậy số sản phẩm đội đó phải làm theo kế hoạch là sản phẩm.