Đại lượng nào đo độ phân tán của nửa giữa của mẫu số liệu, không bị ảnh hưởng nhiều bởi các giá trị ngoại lệ trong mẫu số liệu?
A. Khoảng biến thiên.
B. Khoảng tứ phân vị.
Quảng cáo
Trả lời:
Đáp án đúng là: B
Khoảng tứ phân vị dùng để đo độ phân tán của nửa giữa của mẫu số liệu, không bị ảnh hưởng nhiều bởi các giá trị ngoại lệ trong mẫu số liệu.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số cá bác đã thả trong vụ vừa qua là 20.50 = 1000 con.
Gọi \(x\) là số cá giảm đi, khi đó năng suất \(a\) tăng \(a = \frac{{0,5.x}}{8} = 0,0625x\) (kg/con).
Vậy sản lượng thu được trong năm tới của bác Tôm sẽ là
\(f\left( x \right) = \left( {1000 - x} \right)\left( {1,5 + 0,0625x} \right)\) (kg).
Xét hàm số \(f\left( x \right) = \left( {1000 - x} \right)\left( {1,5 + 0,0625x} \right) = - 0,0625{x^2} + 61x + 1500\).
Có \(f'\left( x \right) = - 0,125x + 61\); \(f'\left( x \right) = 0 \Leftrightarrow x = 488\).
Bảng biến thiên
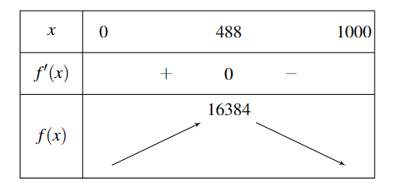
Vậy số cá giống cần mua là \(1000 - 488 = 512\).
Câu 2
Lời giải
Đáp án đúng là: C
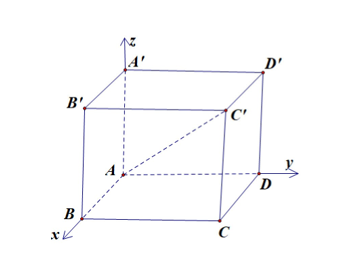
Theo giả thiết có \(\overrightarrow {AB} = 2\,\overrightarrow i \,;\,\,\overrightarrow {AD} = 4\,\overrightarrow j \,;\,\overrightarrow {AA'} = 3\,\overrightarrow k \,;\,\)
Áp dụng quy tắc hình hộp ta có: \(\overrightarrow {AC'} \, = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = 2\,\overrightarrow i \, + 4\overrightarrow j \, + 3\overrightarrow k \).
Do đó điểm \(C'\) có tọa độ là \(\left( {2;4;3} \right)\). Vậy \(a + b - c = 2 + 4 - 3 = 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.