Cho hình chữ nhật \(ABCD\) có hai đỉnh di động trên đồ thị hàm số \(y = 9 - {x^2}\) trên khoảng \(\left( { - 3;3} \right)\), hai đỉnh còn lại nằm trên trục hoành (tham khảo hình vẽ). Tìm diện tích lớn nhất của hình chữ nhật \(ABCD\) (kết quả làm tròn đến hàng phần mười).
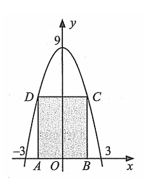
Cho hình chữ nhật \(ABCD\) có hai đỉnh di động trên đồ thị hàm số \(y = 9 - {x^2}\) trên khoảng \(\left( { - 3;3} \right)\), hai đỉnh còn lại nằm trên trục hoành (tham khảo hình vẽ). Tìm diện tích lớn nhất của hình chữ nhật \(ABCD\) (kết quả làm tròn đến hàng phần mười).

Quảng cáo
Trả lời:
Kí hiệu \(x\) là hoành độ của điểm \(B\) \(\left( {0 < x < 3} \right)\).
Ta có \(AB = 2x,BC = 9 - {x^2}\).
Từ đó, diện tích hình chữ nhật \(ABCD\) là \(S\left( x \right) = 18x - 2{x^3},0 < x < 3\).
Ta có \(S'\left( x \right) = 18 - 6{x^2}\), \(S'\left( x \right) = 0 \Leftrightarrow {x^2} = 3 \Leftrightarrow x = \sqrt 3 \) (do \(x > 0\)).
Bảng biến thiên
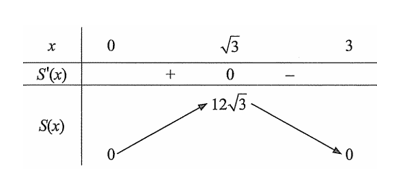
Từ đó \(\mathop {\max }\limits_{\left( {0;3} \right)} S\left( x \right) = S\left( {\sqrt 3 } \right) = 12\sqrt 3 \approx 20,8\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số cá bác đã thả trong vụ vừa qua là 20.50 = 1000 con.
Gọi \(x\) là số cá giảm đi, khi đó năng suất \(a\) tăng \(a = \frac{{0,5.x}}{8} = 0,0625x\) (kg/con).
Vậy sản lượng thu được trong năm tới của bác Tôm sẽ là
\(f\left( x \right) = \left( {1000 - x} \right)\left( {1,5 + 0,0625x} \right)\) (kg).
Xét hàm số \(f\left( x \right) = \left( {1000 - x} \right)\left( {1,5 + 0,0625x} \right) = - 0,0625{x^2} + 61x + 1500\).
Có \(f'\left( x \right) = - 0,125x + 61\); \(f'\left( x \right) = 0 \Leftrightarrow x = 488\).
Bảng biến thiên
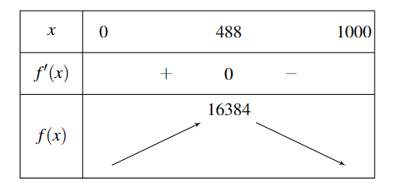
Vậy số cá giống cần mua là \(1000 - 488 = 512\).
Câu 2
Lời giải
Đáp án đúng là: C
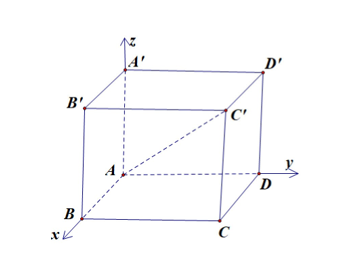
Theo giả thiết có \(\overrightarrow {AB} = 2\,\overrightarrow i \,;\,\,\overrightarrow {AD} = 4\,\overrightarrow j \,;\,\overrightarrow {AA'} = 3\,\overrightarrow k \,;\,\)
Áp dụng quy tắc hình hộp ta có: \(\overrightarrow {AC'} \, = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = 2\,\overrightarrow i \, + 4\overrightarrow j \, + 3\overrightarrow k \).
Do đó điểm \(C'\) có tọa độ là \(\left( {2;4;3} \right)\). Vậy \(a + b - c = 2 + 4 - 3 = 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.