Cho tứ diện đều \(ABCD\) cạnh \(a\). \(E\) là điểm trên đoạn \(CD\) sao cho \(ED = 2CE\).
a) Có \[6\] vectơ (khác vectơ \[\overrightarrow 0 \]) có điểm đầu và điểm cuối được tạo thành từ các đỉnh của tứ diện.
b) Góc giữa hai vectơ \[\overrightarrow {AB\,} \] và \[\overrightarrow {BC\,} \] bằng \[60^\circ \].
c) Nếu \[\overrightarrow {BE\,} = m\overrightarrow {BA\,} + n\overrightarrow {BC\,} + p\overrightarrow {BD\,} \] thì \[m + n + p = \frac{2}{3}\].
d) Tích vô hướng \(\overrightarrow {AD} .\overrightarrow {BE} = \frac{{{a^2}}}{6}\).
Cho tứ diện đều \(ABCD\) cạnh \(a\). \(E\) là điểm trên đoạn \(CD\) sao cho \(ED = 2CE\).
a) Có \[6\] vectơ (khác vectơ \[\overrightarrow 0 \]) có điểm đầu và điểm cuối được tạo thành từ các đỉnh của tứ diện.
b) Góc giữa hai vectơ \[\overrightarrow {AB\,} \] và \[\overrightarrow {BC\,} \] bằng \[60^\circ \].
c) Nếu \[\overrightarrow {BE\,} = m\overrightarrow {BA\,} + n\overrightarrow {BC\,} + p\overrightarrow {BD\,} \] thì \[m + n + p = \frac{2}{3}\].
d) Tích vô hướng \(\overrightarrow {AD} .\overrightarrow {BE} = \frac{{{a^2}}}{6}\).
Quảng cáo
Trả lời:
a) S, b) S, c) S, d) Đ

a) Các vectơ (khác vectơ \[\overrightarrow 0 \]) có điểm đầu và điểm cuối được tạo thành từ các đỉnh của tứ diện là: \[\overrightarrow {AB\,} \],\[\overrightarrow {AC\,} \],\[\overrightarrow {AD\,} \],\[\overrightarrow {BA\,} \],\[\overrightarrow {BC\,} \],\[\overrightarrow {B{\rm{D}}\,} \],\[\overrightarrow {CA\,} \],\[\overrightarrow {CB\,} \],\[\overrightarrow {C{\rm{D}}\,} \],\[\overrightarrow {DA\,} \],\[\overrightarrow {DB\,} \],\[\overrightarrow {DC\,} \].
Do đó có \[12\] vectơ thỏa mãn yêu cầu.
b) \[(\overrightarrow {AB\,} ,\overrightarrow {BC} ) = 180^\circ - (\overrightarrow {BA\,} ,\overrightarrow {BC} ) = 180^\circ - \widehat {ABC} = 120^\circ \].
c) \[\overrightarrow {BE\,} = \overrightarrow {BC\,} + \overrightarrow {CE\,} = \overrightarrow {BC\,} + \frac{1}{3}\overrightarrow {CD\,} = \overrightarrow {BC\,} + \frac{1}{3}\left( {\overrightarrow {BD\,} - \overrightarrow {BC\,} } \right) = \frac{2}{3}\overrightarrow {BC\,} + \frac{1}{3}\overrightarrow {BD\,} \].
Do đó \[m = 0\],\[n = \frac{2}{3}\],\[p = \frac{1}{3}\]. Suy ra \[m + n + p = 1\].
d) Ta có: \(\overrightarrow {BE} = \overrightarrow {AE} - \overrightarrow {AB} = \left( {\overrightarrow {AC} + \overrightarrow {CE} } \right) - \overrightarrow {AB} = \overrightarrow {AC} + \frac{1}{3}\overrightarrow {CD} - \overrightarrow {AB} \)
\( = \overrightarrow {AC} + \frac{1}{3}\left( {\overrightarrow {AD} - \overrightarrow {AC} } \right) - \overrightarrow {AB} = \frac{2}{3}\overrightarrow {AC} + \frac{1}{3}\overrightarrow {AD} - \overrightarrow {AB} \).
Suy ra: \(\overrightarrow {AD} .\overrightarrow {BE} = \overrightarrow {AD} .\left( {\frac{2}{3}\overrightarrow {AC} + \frac{1}{3}\overrightarrow {AD} - \overrightarrow {AB} } \right) = \frac{2}{3}.\overrightarrow {AD} .\overrightarrow {AC} + \frac{1}{3}.{\overrightarrow {AD} ^2} - \overrightarrow {AD} .\overrightarrow {AB} \)
\( = \frac{2}{3}.a.a.\cos 60^\circ + \frac{1}{3}{a^2} - a.a.\cos 60^\circ = \frac{{{a^2}}}{6}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số cá bác đã thả trong vụ vừa qua là 20.50 = 1000 con.
Gọi \(x\) là số cá giảm đi, khi đó năng suất \(a\) tăng \(a = \frac{{0,5.x}}{8} = 0,0625x\) (kg/con).
Vậy sản lượng thu được trong năm tới của bác Tôm sẽ là
\(f\left( x \right) = \left( {1000 - x} \right)\left( {1,5 + 0,0625x} \right)\) (kg).
Xét hàm số \(f\left( x \right) = \left( {1000 - x} \right)\left( {1,5 + 0,0625x} \right) = - 0,0625{x^2} + 61x + 1500\).
Có \(f'\left( x \right) = - 0,125x + 61\); \(f'\left( x \right) = 0 \Leftrightarrow x = 488\).
Bảng biến thiên
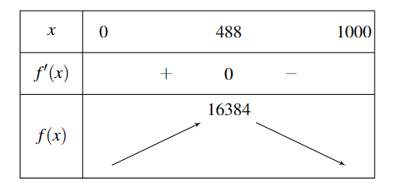
Vậy số cá giống cần mua là \(1000 - 488 = 512\).
Câu 2
Lời giải
Đáp án đúng là: C
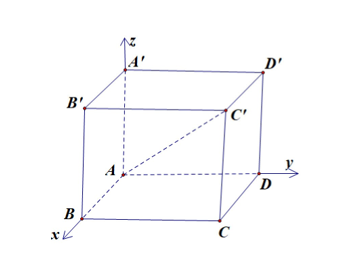
Theo giả thiết có \(\overrightarrow {AB} = 2\,\overrightarrow i \,;\,\,\overrightarrow {AD} = 4\,\overrightarrow j \,;\,\overrightarrow {AA'} = 3\,\overrightarrow k \,;\,\)
Áp dụng quy tắc hình hộp ta có: \(\overrightarrow {AC'} \, = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = 2\,\overrightarrow i \, + 4\overrightarrow j \, + 3\overrightarrow k \).
Do đó điểm \(C'\) có tọa độ là \(\left( {2;4;3} \right)\). Vậy \(a + b - c = 2 + 4 - 3 = 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.