Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình sau. Phương trình \[f\left( {f\left( x \right)} \right) = 0\] có bao nhiêu nghiệm thực phân biệt?
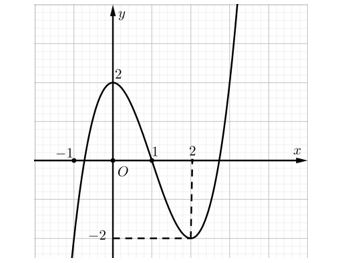
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình sau. Phương trình \[f\left( {f\left( x \right)} \right) = 0\] có bao nhiêu nghiệm thực phân biệt?

Quảng cáo
Trả lời:
Dựa vào đồ thị ta có \[f\left( {f\left( x \right)} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a\,\,\,\,\left( { - 1 < a < 0} \right)\\f\left( x \right) = 1\\f\left( x \right) = b\,\,\,\,\left( {2 < b < 3} \right)\end{array} \right.\] .
Phương trình \[f\left( x \right) = a\] với \[ - 1 < a < 0\] có ba nghiệm thực phân biệt.
Phương trình \[f\left( x \right) = 1\] có ba nghiệm thực phân biệt.
Phương trình \[f\left( x \right) = b\] với \[2 < b < 3\] có một nghiệm .
Vậy phương trình \[f\left( {f\left( x \right)} \right) = 0\] có \(7\) nghiệm thực phân biệt.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số cá bác đã thả trong vụ vừa qua là 20.50 = 1000 con.
Gọi \(x\) là số cá giảm đi, khi đó năng suất \(a\) tăng \(a = \frac{{0,5.x}}{8} = 0,0625x\) (kg/con).
Vậy sản lượng thu được trong năm tới của bác Tôm sẽ là
\(f\left( x \right) = \left( {1000 - x} \right)\left( {1,5 + 0,0625x} \right)\) (kg).
Xét hàm số \(f\left( x \right) = \left( {1000 - x} \right)\left( {1,5 + 0,0625x} \right) = - 0,0625{x^2} + 61x + 1500\).
Có \(f'\left( x \right) = - 0,125x + 61\); \(f'\left( x \right) = 0 \Leftrightarrow x = 488\).
Bảng biến thiên
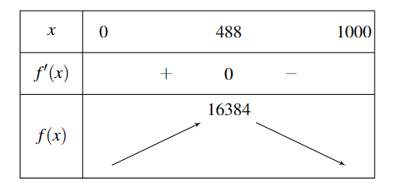
Vậy số cá giống cần mua là \(1000 - 488 = 512\).
Câu 2
Lời giải
Đáp án đúng là: C
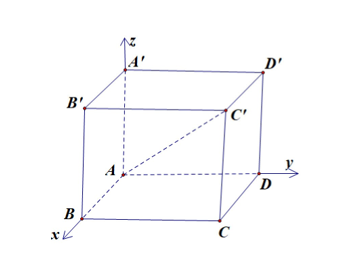
Theo giả thiết có \(\overrightarrow {AB} = 2\,\overrightarrow i \,;\,\,\overrightarrow {AD} = 4\,\overrightarrow j \,;\,\overrightarrow {AA'} = 3\,\overrightarrow k \,;\,\)
Áp dụng quy tắc hình hộp ta có: \(\overrightarrow {AC'} \, = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = 2\,\overrightarrow i \, + 4\overrightarrow j \, + 3\overrightarrow k \).
Do đó điểm \(C'\) có tọa độ là \(\left( {2;4;3} \right)\). Vậy \(a + b - c = 2 + 4 - 3 = 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.