Bộ 10 đề thi cuối kì 1 Toán 12 Chân trời sáng tạo có đáp án (Đề 4)
49 người thi tuần này 4.6 5.5 K lượt thi 22 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Đề ôn luyện Toán Chương 8. Một số yếu tố thống kê, xác suất và lý thuyết đồ thị (đề số 3)
237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải (P1)
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
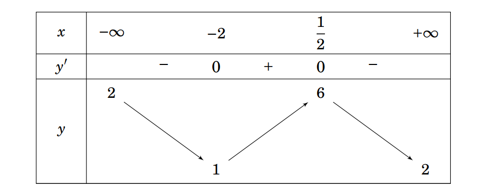
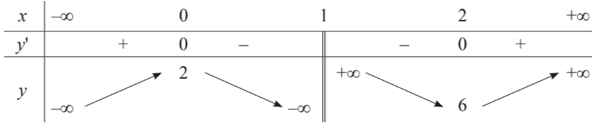
A. Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trong khoảng \(\left( { - \infty ; - 2} \right)\) là \(1\) .
B. Giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trong khoảng \(\left( { - \infty ;\frac{1}{2}} \right)\) là \(6\).
C. Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trong khoảng \(\left( { - 2;\frac{1}{2}} \right)\) là \(1\).
Lời giải
Đáp án đúng là: D
Dựa vào bẳng biến thiên ta thấy hàm số \(y = f\left( x \right)\) không có giá trị nhỏ nhất trên khoảng \(\left( { - 2; + \infty } \right)\)
Câu 2
Lời giải
Đáp án đúng là: D
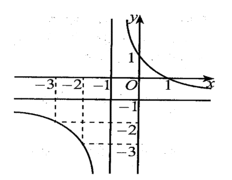
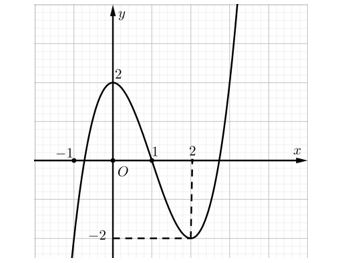
Từ đồ thị hàm số ta suy ra \(y = - 1\) là tiệm cận ngang của đồ thị hàm số.
Câu 3
A. \(y = \frac{{{x^2} + 2x - 2}}{{x - 1}}\).
Lời giải
Đáp án đúng là: A
Dựa vào bảng biến thiên ta thấy đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = 1\). Suy ra loại B và D.
Ta thấy đồ thị hàm số đi qua điểm \(\left( {0;2} \right)\) nên loại C.
Vậy bảng biến thiên đề bài cho là của hàm số \(y = \frac{{{x^2} + 2x - 2}}{{x - 1}}\).
Câu 4
Lời giải
Đáp án đúng là: A
Ta có \(y' = {x^2} + 2x - m\).
Hàm số \(y = \frac{1}{3}{x^3} + {x^2} - mx - 1\) có đúng một điểm cực trị thuộc khoảng \(\left( {0;4} \right)\) khi phương trình \(y' = 0\) chỉ có đúng một nghiệm thuộc khoảng \(\left( {0;4} \right)\).
Ta có \(y' = 0 \Leftrightarrow {x^2} + 2x = m\) (*)
Bảng biến thiên của hàm số \(f\left( x \right) = {x^2} + 2x\) trên khoảng \(\left( {0;4} \right)\) như sau:
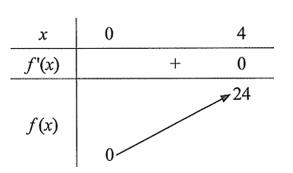
Dựa vào bảng biến thiên, ta thấy phương trình (*) có đúng một nghiệm thuộc khoảng \(\left( {0;4} \right)\) khi \(0 < m < 24\).
Vì \(m \in \mathbb{Z}\) nên \(m \in \left\{ {1;2;3;...;23} \right\}\).
Vậy có 23 giá trị nguyên của \(m\) thỏa mãn yêu cầu.
Câu 5
Lời giải
Đáp án đúng là: B
\(\overrightarrow {OA} = \left( {3; - 4;0} \right)\).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
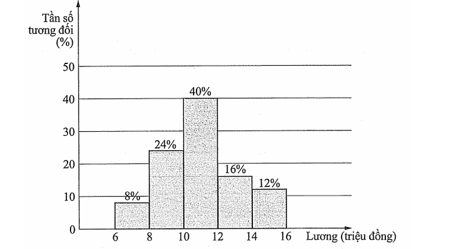
Câu 11
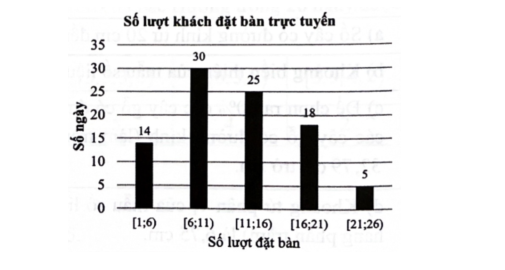
A. Khoảng biến thiên.
B. Khoảng tứ phân vị.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
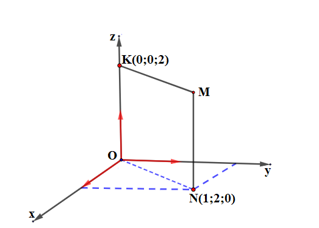
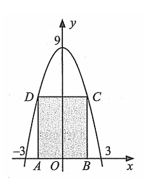
![Phần mái của một căn nhà có dạng là khối đa diện được mô tả và gắn trên hệ trục tọa độ \[Oxyz\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/12/blobid14-1733932800.png)