Người ta muốn xây một cái bể hình hộp đứng có thể tích \(V = 18\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\), biết đáy bể là hình chữ nhật có chiều dài gấp \(3\) lần chiều rộng và bể không có nắp. Hỏi cần xây bể có chiều cao \(h\) bằng bao nhiêu mét để nguyên vật liệu xây dựng là ít nhất?
Người ta muốn xây một cái bể hình hộp đứng có thể tích \(V = 18\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\), biết đáy bể là hình chữ nhật có chiều dài gấp \(3\) lần chiều rộng và bể không có nắp. Hỏi cần xây bể có chiều cao \(h\) bằng bao nhiêu mét để nguyên vật liệu xây dựng là ít nhất?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \(x\)\(\left( {x > 0} \right)\) là chiều rộng hình chữ nhật đáy bể, suy ra chiều dài hình chữ nhật đáy bể là \(3x.\)
\(V = h.x.3x = h.3{x^2} = 18\) \( \Rightarrow h = \frac{{18}}{{3{x^2}}} = \frac{6}{{{x^2}}}\).
Gọi \(P\) là diện tích xung quanh cộng với diện tích một đáy bể của hình hộp chữ nhật.
Nguyên vật liệu ít nhất khi \(P\) nhỏ nhất.
\(P = 2hx + 2.h.3x + 3{x^2} = 2.\frac{6}{{{x^2}}}.x + 2.\frac{6}{{{x^2}}}.3x + 3{x^2} = \frac{{48}}{x} + 3{x^2}.\)
Đặt \(f\left( x \right) = \frac{{48}}{x} + 3{x^2}\), \(\left( {x > 0} \right)\).
Ta có hàm số \(f\left( x \right)\) liên tục trên \(\left( {0; + \infty } \right)\)
và \(f'\left( x \right) = \frac{{ - 48}}{{{x^2}}} + 6x\),\(f'\left( x \right) = 0 \Leftrightarrow \frac{{ - 48}}{{{x^2}}} + 6x = 0 \Leftrightarrow {x^3} = 8 \Leftrightarrow x = 2\).
Bảng biến thiên:
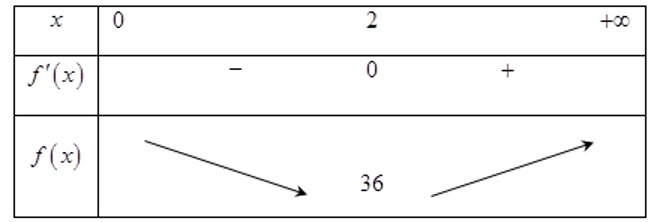
Suy ra vật liệu ít nhất khi \(h = \frac{6}{{{x^2}}} = \frac{6}{4} = 1,5\left( {\rm{m}} \right)\).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vị trí của máy bay sau 5 phút tiếp theo là \(C(x;y;z)\).
Vì hướng của máy bay không đổi nên \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) cùng hướng.
Do vận tốc của máy bay không đổi và thời gian bay từ \(A\) đến \(B\) gấp đôi thời gian bay từ \(B\) đến \(C\) nên \(AB = 2BC\).
Do đó \(\overrightarrow {BC} = \frac{1}{2}\overrightarrow {AB} = \left( {\frac{{940 - 800}}{2};\frac{{550 - 500}}{2};\frac{{9 - 7}}{2}} \right) = \left( {70;25;1} \right)\).
Mặt khác, \(\overrightarrow {BC} = (x - 940;y - 550;z - 9)\) nên \(\left\{ {\begin{array}{*{20}{l}}{x - 940 = 70}\\{y - 550 = 25}\\{z - 9 = 1}\end{array}} \right.\)
Từ đó \(\left\{ {\begin{array}{*{20}{l}}{x = 1010}\\{y = 575}\\{z = 10}\end{array}} \right. \Rightarrow x + y + z = 1595\).
Lời giải
a) S, b) S, c) Đ, d) S
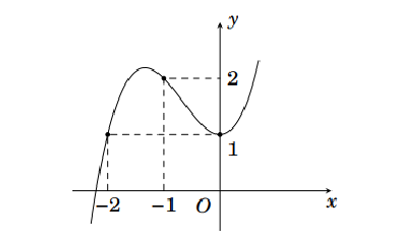
a) Dựa vào đồ thị ta thấy hàm số đồng biến trên khoảng \(\left( { - \infty ;{x_0}} \right)\) với \( - 2 < {x_0} < - 1\).
b) Hàm số đạt cực tiểu tại \(x = 0,{y_{CT}} = 1\).
c) Đồ thị hàm số cắt trục Oy tại điểm có tọa độ \(\left( {0;1} \right)\).
d) Đồ thị đi qua ba điểm \(\left( { - 2;1} \right),\left( { - 1;2} \right),\left( {0;1} \right)\) và đạt cực trị tại \(x = 1\) nên ta có hệ:
\(\left\{ \begin{array}{l} - 8a + 4b - 2c + d = 1\\ - a + b - c + d = 2\\d = 1\\c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c = 0\\d = 1\end{array} \right. \Rightarrow 2a + 3b + c = 8\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
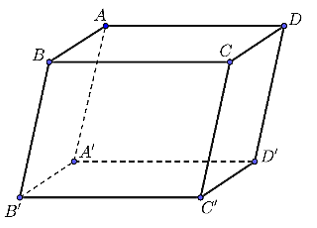
A. \(2\overrightarrow {AA'} \).
B. \(\overrightarrow 0 \).
C. \(2\overrightarrow {AC} \).
D. \(2\overrightarrow {C'A'} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo