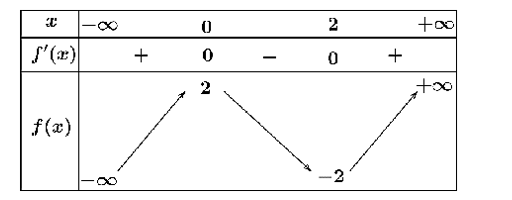
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
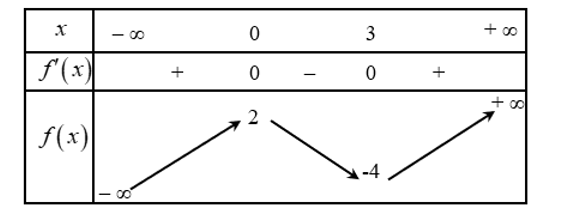
Đồ thị hàm số \(y = f\left( x \right)\) có điểm cực tiểu là
Quảng cáo
Trả lời:
Đáp án đúng là: B
Dựa vào bảng biến thiên, ta có đồ thị hàm số \(y = f\left( x \right)\) có điểm cực tiểu là \(\left( {3\,;\, - 4} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đ, b) S, c) S, d) S
a) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
b) Ta có \(g'\left( x \right) = 2 - 3f'\left( x \right) > 0,\forall x \in \left( {0;2} \right)\), suy ra hàm số \(g\left( x \right) = 2x - 3f\left( x \right)\) đồng biến trên khoảng \(\left( {0;2} \right)\).
c) Ta có hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng \(\left( {0;2} \right)\).
Mà \(0 \le {\sin ^2}x \le 1,\forall x \in \mathbb{R}\)\( \Rightarrow 0 \le {\sin ^2}x < \frac{3}{2},\forall x \in \mathbb{R}\) \( \Rightarrow f\left( {{{\sin }^2}x} \right) > f\left( {\frac{3}{2}} \right)\).
d) Ta có \(y' = {\left( {2 - 3x} \right)^\prime } \cdot f'\left( {2 - 3x} \right) = - 3f'\left( {2 - 3x} \right)\).
Hàm số \(y = f\left( {2 - 3x} \right)\) nghịch biến \(y' = - 3f'\left( {2 - 3x} \right) < 0 \Leftrightarrow f'\left( {2 - 3x} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}2 - 3x < 0\\2 - 3x > 2\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x > \frac{2}{3}\\x < 0\end{array} \right.\). Suy ra hàm số \(y = f\left( {2 - 3x} \right)\) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {\frac{2}{3}; + \infty } \right)\).
Lời giải
Ta có \(M \in \left( C \right)\) \( \Rightarrow M\left( {{x_0};{x_0} + \frac{1}{{{x_0} + 1}}} \right)\) với \({x_0} > - 1\).
Ta có \(I{M^2} = {\left( {{x_0} + 1} \right)^2} + {\left( {{x_0} + 1 + \frac{1}{{{x_0} + 1}}} \right)^2} = 2{\left( {{x_0} + 1} \right)^2} + \frac{1}{{{{\left( {{x_0} + 1} \right)}^2}}} + 2\).
Đặt \(t = {\left( {{x_0} + 1} \right)^2},t > 0\) thì khi đó \(I{M^2} = 2t + 2 + \frac{1}{t}\).
Xét hàm số \(y = 2t + 2 + \frac{1}{t}\) có \(y' = 2 - \frac{1}{{{t^2}}} = 0 \Leftrightarrow t = \frac{1}{{\sqrt 2 }}\).
Bảng biến thiên
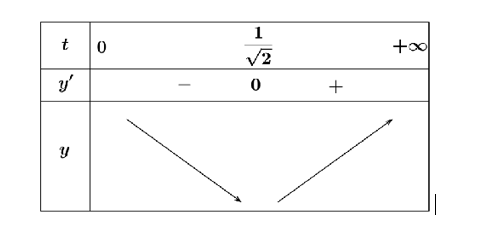
Để thuyền thu được sóng tốt nhất \( \Leftrightarrow IM\) ngắn nhất \( \Leftrightarrow {x_0} = \frac{1}{{\sqrt[4]{2}}} - 1\).
Vậy \(n = 4;a = 2;b = 1 \Rightarrow a \cdot n + b = 9\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Hàm số nghịch biến trên khoảng \(\left( { - 1;\,1} \right) \cup \left( {1\,;\,3} \right)\).
B. Hàm số nghịch biến trên khoảng \(\left( { - 1;\,3} \right){\rm{\backslash }}\left\{ 1 \right\}\).
C. Hàm số nghịch biến trên mỗi khoảng \(\left( { - 1;\,1} \right)\)và \(\left( {1\,;\,3} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.