Xí nghiệp \(A\) sản xuất độc quyền một loại sản phẩm. Biết rằng hàm tổng chi phí sản xuất là \(TC = {x^3} - 77{x^2} + 1000x + 4000\) và hàm doanh thu là \(TR = - 2{x^2} + 1312x\), với \(x\) là số sản phẩm. Lợi nhuận của xí nghiệp \(A\) được xác định bằng hàm số \(f\left( x \right) = TR - TC\), cực đại lợi nhuận của xí nghiệp \(A\) khi đó đạt bao nhiêu sản phẩm?
Xí nghiệp \(A\) sản xuất độc quyền một loại sản phẩm. Biết rằng hàm tổng chi phí sản xuất là \(TC = {x^3} - 77{x^2} + 1000x + 4000\) và hàm doanh thu là \(TR = - 2{x^2} + 1312x\), với \(x\) là số sản phẩm. Lợi nhuận của xí nghiệp \(A\) được xác định bằng hàm số \(f\left( x \right) = TR - TC\), cực đại lợi nhuận của xí nghiệp \(A\) khi đó đạt bao nhiêu sản phẩm?
Quảng cáo
Trả lời:
Xét hàm số:
\(f\left( x \right) = TR - TC = - 2{x^2} + 1312x - \left( {{x^3} - 77{x^2} + 1000x + 4000} \right)\).
\(f\left( x \right) = - {x^3} + 75{x^2} + 312x - 4000\).
TXĐ: \(D = \left( {0\,;\, + \infty } \right)\).
Ta có \(f'\left( x \right) = - 3{x^2} + 150x + 312 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 52\left( N \right)\\x = - 2\left( L \right)\end{array} \right.\).
Bảng biến thiên:
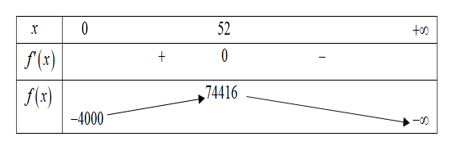
Hàm số đạt giá trị cực đại tại \(x = 52\).
Vậy lợi nhuận của công ty đạt cực đại khi số sản phẩm \(x = 52\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
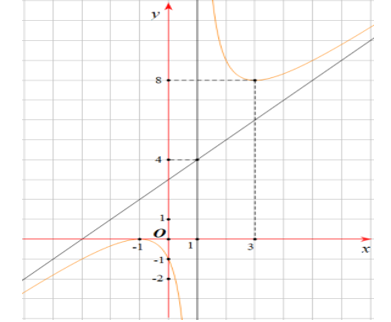
Vì điểm \(A'\) có toạ độ là \(\left( {240;450;0} \right)\) nên khoảng cách từ \(A'\) đến các trục \(Ox,Oy\) lần lượt là \(450\;{\rm{cm}}\) và \(240\;{\rm{cm}}\). Suy ra \(A'A = 450\;{\rm{cm}}\) và \(A'O' = 240\;{\rm{cm}}\).
Từ giả thiết suy ra \(\overrightarrow {A'B'} = \left( { - 120;0;300} \right)\),
do đó \(A'B' = \left| {\overrightarrow {A'B'} } \right| = \sqrt {{{( - 120)}^2} + {0^2} + {{300}^2}} = 60\sqrt {29} \approx 323(\;{\rm{cm}})\).
Vì \(O'O = A'A = 450\;{\rm{cm}}\) và \(O'\) nằm trên trục \[Oy\] nên toạ độ của điểm \(O'\) là \(\left( {0;450;0} \right)\).
Do đó \(\overline {O'B'} = \left( {120;0;300} \right)\) và \(O'B' = \left| {\overline {O'B'} } \right| = \sqrt {{{120}^2} + {0^2} + {{300}^2}} = 60\sqrt {29} \approx 323{\rm{ }}({\rm{cm}})\).
Vậy mỗi căn lều gỗ có chiều dài là \(450\;{\rm{cm}}\), chiều rộng là \(240\;{\rm{cm}}\), mỗi cạnh bên của mặt tiền có độ dài là 323 cm.
\( \Rightarrow a + b + c = 1013\).
Lời giải
Ta có \(N'\left( t \right) = - 3{t^2} + 24t = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 8\end{array} \right.\).
Bảng biến thiên
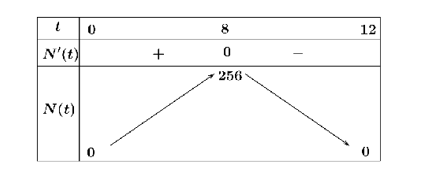
Từ bảng biến thiên ta thấy số người bị nhiễm bệnh tăng trong khoảng thời gian \(\left( {0;8} \right)\).
Suy ra \(a = 0;b = 8\). Vậy \(a + b = 8\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.