Câu hỏi:
12/12/2024 3,052
Trong không gian \(Oxyz\), cho tam giác \(ABC\) với \(A\left( {1;2;5} \right),B\left( {2;4; - 3} \right),C\left( {3;3;1} \right)\). Gọi \(G\) là trọng tâm của tam giác \(ABC\) và \(M\) là điểm thay đổi trên mặt phẳng \(\left( {Oxy} \right)\). Độ dài \(GM\) ngắn nhất bằng bao nhiêu?
Trong không gian \(Oxyz\), cho tam giác \(ABC\) với \(A\left( {1;2;5} \right),B\left( {2;4; - 3} \right),C\left( {3;3;1} \right)\). Gọi \(G\) là trọng tâm của tam giác \(ABC\) và \(M\) là điểm thay đổi trên mặt phẳng \(\left( {Oxy} \right)\). Độ dài \(GM\) ngắn nhất bằng bao nhiêu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
\(G\) là trọng tâm tam giác \(ABC\), suy ra \(G\left( {2;3;1} \right)\).
Gọi \(H\) là hình chiếu vuông góc của \(G\) trên mặt phẳng \(\left( {Oxy} \right)\). Khi đó \(GH\) là khoảng cách từ \(G\) đến mặt phẳng \(\left( {Oxy} \right)\), ta có \(GH = d\left( {G,\left( {Oxy} \right)} \right) = 1\).
Với \(M\) là điểm thay đổi trên mặt phẳng \(\left( {Oxy} \right)\), ta có \(GM \ge GH = 1\).
Do đó \(GM\) ngắn nhất \( \Leftrightarrow M \equiv H\). Vậy độ dài \(GM\) ngắn nhất bằng 1.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
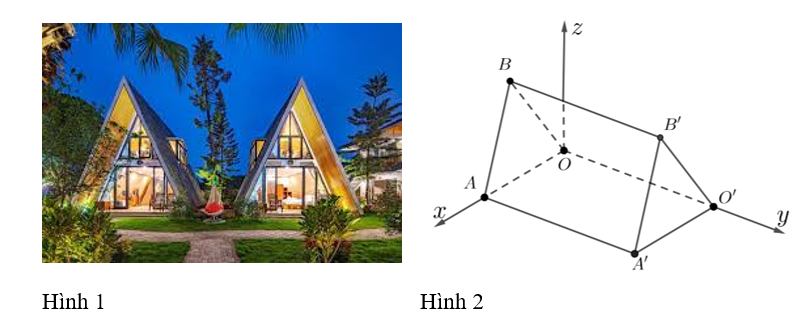
Vì điểm \(A'\) có toạ độ là \(\left( {240;450;0} \right)\) nên khoảng cách từ \(A'\) đến các trục \(Ox,Oy\) lần lượt là \(450\;{\rm{cm}}\) và \(240\;{\rm{cm}}\). Suy ra \(A'A = 450\;{\rm{cm}}\) và \(A'O' = 240\;{\rm{cm}}\).
Từ giả thiết suy ra \(\overrightarrow {A'B'} = \left( { - 120;0;300} \right)\),
do đó \(A'B' = \left| {\overrightarrow {A'B'} } \right| = \sqrt {{{( - 120)}^2} + {0^2} + {{300}^2}} = 60\sqrt {29} \approx 323(\;{\rm{cm}})\).
Vì \(O'O = A'A = 450\;{\rm{cm}}\) và \(O'\) nằm trên trục \[Oy\] nên toạ độ của điểm \(O'\) là \(\left( {0;450;0} \right)\).
Do đó \(\overline {O'B'} = \left( {120;0;300} \right)\) và \(O'B' = \left| {\overline {O'B'} } \right| = \sqrt {{{120}^2} + {0^2} + {{300}^2}} = 60\sqrt {29} \approx 323{\rm{ }}({\rm{cm}})\).
Vậy mỗi căn lều gỗ có chiều dài là \(450\;{\rm{cm}}\), chiều rộng là \(240\;{\rm{cm}}\), mỗi cạnh bên của mặt tiền có độ dài là 323 cm.
\( \Rightarrow a + b + c = 1013\).
Lời giải
Ta có \(N'\left( t \right) = - 3{t^2} + 24t = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 8\end{array} \right.\).
Bảng biến thiên
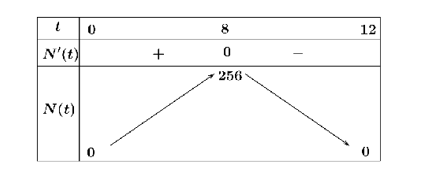
Từ bảng biến thiên ta thấy số người bị nhiễm bệnh tăng trong khoảng thời gian \(\left( {0;8} \right)\).
Suy ra \(a = 0;b = 8\). Vậy \(a + b = 8\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận