Một ô tô đang chạy đều với vận tốc \(a\left( {{\rm{m/s}}} \right)\) thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) = - 5t + a\left( {{\rm{m/s}}} \right)\), trong đó \(t\) là thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi vận tốc ban đầu \(a\) của ô tô là bao nhiêu (m/s), biết từ lúc đạp phanh đến khi dừng hẳn ô tô di chuyển được 40 mét.
Một ô tô đang chạy đều với vận tốc \(a\left( {{\rm{m/s}}} \right)\) thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) = - 5t + a\left( {{\rm{m/s}}} \right)\), trong đó \(t\) là thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi vận tốc ban đầu \(a\) của ô tô là bao nhiêu (m/s), biết từ lúc đạp phanh đến khi dừng hẳn ô tô di chuyển được 40 mét.
Quảng cáo
Trả lời:
Ô tô dừng hẳn khi \(v\left( t \right) = - 5t + a = 0 \Leftrightarrow t = \frac{a}{5}\).
Vì \(\int\limits_0^{\frac{a}{5}} {v\left( t \right)dt} = 40\) nên \(\int\limits_0^{\frac{a}{5}} {\left( { - 5t + a} \right)dt} = 40\)\( \Leftrightarrow \left. {\left( {\frac{{ - 5}}{2}{t^2} + at} \right)} \right|_0^{\frac{a}{5}} = 40\)
\( \Leftrightarrow - \frac{{{a^2}}}{{10}} + \frac{{{a^2}}}{5} = 40\)\( \Leftrightarrow \frac{{{a^2}}}{{10}} = 40\)\( \Leftrightarrow a = 20\).
Vậy vận tốc ban đầu của ô tô là 20 m/s.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) S, b) Đ, c) Đ, d) Đ
a) Có \(s\left( t \right) = \int {v\left( t \right)dt} = \int {\left( {2,01t - 0,025{t^2}} \right)dt} = 1,005{t^2} - \frac{{{t^3}}}{{120}} + C\).
Vì \(s\left( 0 \right) = 0 \Rightarrow C = 0\). Do đó \(s\left( t \right) = 1,005{t^2} - \frac{{{t^3}}}{{120}}\).
b) Quãng đường xe di chuyển trong 3 giây là:
\(s = \int\limits_0^3 {\left( {2,01t - 0,025{t^2}} \right)dt} = \left. {\left( {1,005{t^2} - \frac{{{t^3}}}{{120}}} \right)} \right|_0^3 = 8,82\).
c) Quãng đường xe di chuyển trong giây thứ 9 là:
\(s = \int\limits_8^9 {\left( {2,01t - 0,025{t^2}} \right)dt} = \left. {\left( {1,005{t^2} - \frac{{{t^3}}}{{120}}} \right)} \right|_8^9 \approx 15,277\).
d) Ta có \(v\left( t \right) = 2,01t - 0,025{t^2}\left( {0 \le t \le 10} \right)\)\( \Rightarrow \mathop {\max }\limits_{\left[ {0;10} \right]} v\left( t \right) = 17,6\;{\rm{m/s}}\) khi \(t = 10{\rm{s}}\).
Gia tốc vật khi đó là \(a\left( {10} \right) = v'\left( {10} \right) = 2,01 - 0,05.10 = 1,51\)(m/s2).
Lời giải
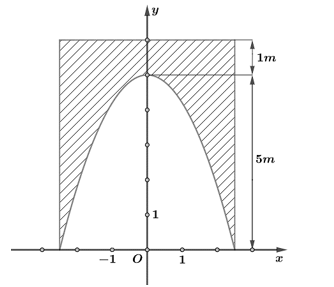
Chọn hệ trục tọa độ như hình vẽ, khi đó \(\left( P \right)\) có phương trình dạng: \(y = a{x^2} + b\).
Khi đó: \(\left( {\frac{5}{2};0} \right)\,;\,\left( {0;5} \right) \in \left( P \right)\) nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}0 = a.{\left( {\frac{5}{2}} \right)^2} + b\\5 = b\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{ - 4}}{5}\\b = 5\end{array} \right.\) hay \(\left( P \right):y = - \frac{4}{5}{x^2} + 5\).
Khi đó diện tích phần cổng \(\left( P \right)\) là: \({S_1} = \int\limits_{ - \frac{5}{2}}^{\frac{5}{2}} {\left( { - \frac{4}{5}{x^2} + 5} \right)dx} = \frac{{50}}{3}\).
Suy ra diện tích phần cần trang trí là: \({S_2} = 5.6 - \frac{{50}}{3} = \frac{{40}}{3}\).
Vậy số tiền cần dùng để trang trí là: \(T = 1\,200\,000.\,\,\frac{{40}}{3} = 16\,000\,000\)(đồng) = 16 triệu đồng.
Câu 3
A. \(2\ln \left( {x + 1} \right) + \frac{2}{{x + 1}} + C\).
B. \(2\ln \left( {x + 1} \right) + \frac{3}{{x + 1}} + C\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(x + 2y - 5z = 0\).
B. \(x + 2y - 5z + 1 = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.