Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ {a;b} \right]\) và \(f\left( a \right) = 2,f\left( b \right) = - 4\). Tính \(T = \int\limits_a^b {f'\left( x \right)dx} \).
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ {a;b} \right]\) và \(f\left( a \right) = 2,f\left( b \right) = - 4\). Tính \(T = \int\limits_a^b {f'\left( x \right)dx} \).
Quảng cáo
Trả lời:
Đáp án đúng là: A
\(T = \int\limits_a^b {f'\left( x \right)dx} = \left. {f\left( x \right)} \right|_a^b = f\left( b \right) - f\left( a \right) = - 4 - 2 = - 6\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Mặt phẳng \(\left( \beta \right)\) song song với mặt phẳng \(\left( \alpha \right)\) nên mặt phẳng \(\left( \beta \right)\) có dạng:\(x - 2y + 2z + d = 0\left( {d \ne 2} \right)\).
Có \(d\left( {M,\left( \beta \right)} \right) = 1 \Leftrightarrow \frac{{\left| {1 - 2.2 + 2.\left( { - 1} \right) + d} \right|}}{{\sqrt {{1^2} + {{\left( { - 2} \right)}^2} + {2^2}} }} = 1 \Leftrightarrow \left| {d - 5} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}d = 8\left( {TM} \right)\\d = 2\left( {KTM} \right)\end{array} \right.\).
Do đó \(\left( \beta \right):x - 2y + 2z + 8 = 0\). Suy ra \(b = 2;c = 2;d = 8\).
Vậy \(S = 3.2 - 2 + 8 = 12\).
Lời giải
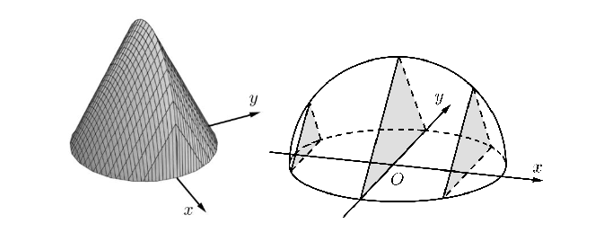
Bán kính đường tròn là 4.
Vì cắt vật bởi các mặt phẳng vuông góc với trục \(Ox\) tại \(x\left( { - 4 \le x \le 4} \right)\).
Suy ra cạnh của tam giác đều là \(2\sqrt {16 - {x^2}} \).
Do đó diện tích tam giác đều là \(S = \frac{{\sqrt 3 }}{4}{\left( {2\sqrt {16 - {x^2}} } \right)^2} = \sqrt 3 \left( {16 - {x^2}} \right)\).
Thể tích vật thể là \(V = \int\limits_{ - 4}^4 {\left[ {\sqrt 3 \left( {16 - {x^2}} \right)} \right]dx} = \frac{{256\sqrt 3 }}{3}\).
Suy ra \(a = 256;b = 3\). Do đó \(a + b = 259\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[2x + 3y - 6z + 1 = 0\].
B. \[3x + 2y - 6z + 1 = 0\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{x}{3} + \frac{y}{{ - 1}} + \frac{z}{2} = 1\).
B. \(\frac{x}{3} + \frac{y}{1} + \frac{z}{{ - 2}} = 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.