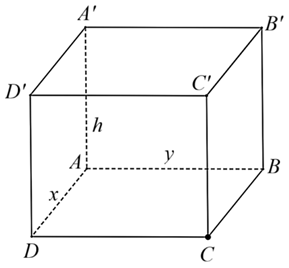
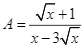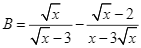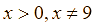Nam làm một chiếc hộp không nắp dạng hình hộp chữ nhật bằng bìa carton có thể tích 3 dm3. Biết tỉ số giữa chiều cao h và chiều rộng đáy y bằng 4. Xác định chiều dài x để lượng bìa cần sử dụng là ít nhấ

Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Theo đề bài, tỉ số giữa chiều cao \(h\) và chiều rộng đáy \(y\) bằng \(4\) nên \(h = 4y\).
Thể tích chiếc hộp \(3{\rm{ d}}{{\rm{m}}^3}\) nên \(xyh = 3{\rm{ }}\left( {{\rm{d}}{{\rm{m}}^3}} \right)\) hay \(4x{y^2} = 3\), suy ra \(x = \frac{3}{{4{y^2}}}\).
Do chiếc hộp không nắp, do đó diện tích bìa cần dùng là tổng diện tích đáy hộp và diện tích xung quanh của hộp.
Ta có: \(S = xy + 2h\left( {x + y} \right) = \frac{3}{{4{y^2}}} \cdot y + 2 \cdot 4y \cdot \left( {\frac{3}{{4{y^2}}} + y} \right)\)
\( = \frac{3}{{4y}} + \frac{6}{y} + 8{y^2} = \frac{{27}}{{4y}} + 8{y^2} = \frac{{27}}{{8y}} + \frac{{27}}{{8y}} + 8{y^2}\).
Do \(y\) là chiều rộng của hộp nên \(y > 0\).
Do đó, áp dụng bất đẳng thức Cauchy cho ba số \(\frac{{27}}{{8y}}\,;\,\,\frac{{27}}{{8y}}\,;\,\,8{y^2}\) không âm, ta được:
\(\frac{{27}}{{8y}} + \frac{{27}}{{8y}} + 8{y^2} \ge 3 \cdot \sqrt[3]{{\frac{{27}}{{8y}} \cdot \frac{{27}}{{8y}} \cdot 8{y^2}}}\), suy ra \(S \ge \frac{{27}}{2}.\)
Dấu “=” xảy ra khi và chỉ khi \(\frac{{27}}{{8y}} = 8{y^2}\) hay \({y^3} = \frac{{27}}{{64}}\) nên \(y = \frac{3}{4}\) (dm).
Do đó, \(x = \frac{3}{{4{y^2}}} = \frac{3}{{4 \cdot {{\left( {\frac{3}{4}} \right)}^2}}} = \frac{4}{3}{\rm{ }}\left( {{\rm{dm}}} \right)\).
Vậy lượng bìa cần dùng ít nhất có diện tích là \(\frac{{27}}{2}{\rm{ }}\left( {{\rm{d}}{{\rm{m}}^2}} \right)\) khi chiều dài \(x = \frac{4}{3}\) dm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\,\,({\rm{ml}})\) là thể tích dung dịch nước muối \(1,5\% \) và \(y\,\,({\rm{ml}})\) là thể tích nước cất \(0\% \) \[\left( {x,\,\,y > 0} \right).\]
Tổng thể tích dung dịch là \(1{\rm{ 000 ml}}\) nên ta có phương trình \(x + y = 1000\) (1).
Tổng khối lượng muối trong dung dịch là \(0,9\% \) của \(1{\rm{ 000 ml}}\). Lượng muối trong dung dịch ban đầu là \(1,5\% .x\) và trong nước cất là \(0\).
Do đó: \(0,015x + 0y = 0,009.1000\) hay \(0,015x = 9\) (2).
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 1000\\0,015x = 9\end{array} \right.\).
Giải phương trình \(0,015x = 9\) được \(x = 9:0,015 = 600\) (thỏa mãn).
Thay \(x = 600\) vào phương trình (1), được: \(y = 1000 - 600 = 400\) (thỏa mãn).
Vậy Lan cần \(600{\rm{ ml}}\) dung dịch nước muối \(1,5\% \) và \(400{\rm{ ml}}\) dung dịch nước cốt \(0\% \) để pha được dung dịch mong muốn.
Lời giải
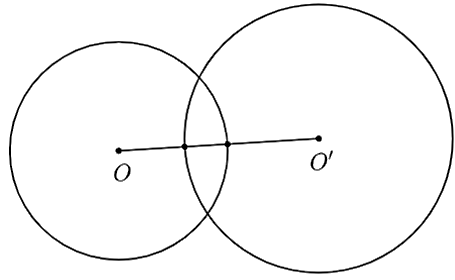
Đáp án đúng là: C
Khi R - R' < OO' < R + R' thì hai đường tròn đó cắt nhau. Do đó, số điểm chung là 2 điểm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.