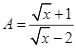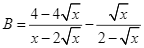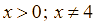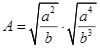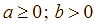Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Với 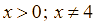 , ta có:
, ta có: 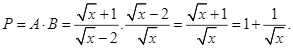
Với ![]() để
để ![]() nhận giá trị nguyên thì
nhận giá trị nguyên thì ![]() là nhận giá trị nguyên hay
là nhận giá trị nguyên hay ![]() .
.
Do đó, ![]() là ước của
là ước của ![]()
Mà ![]() nên
nên ![]() hay
hay ![]() (thỏa mãn).
(thỏa mãn).
Vậy ![]() thì
thì ![]() nhận giá trị nguyên.
nhận giá trị nguyên.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi ![]() (giờ) là thời gian để vòi thứ nhất chảy một mình đầy bể;
(giờ) là thời gian để vòi thứ nhất chảy một mình đầy bể;
![]() (giờ) là thời gian để vòi thứ hai chảy một mình đầy bể (
(giờ) là thời gian để vòi thứ hai chảy một mình đầy bể (![]() ).
).
Đổi: 1 giờ 20 phút = ![]() giờ, 12 phút =
giờ, 12 phút = ![]() giờ, 10 phút =
giờ, 10 phút = ![]() giờ.
giờ.
Theo đề, hai vòi cùng chảy thì sau ![]() giờ sẽ đầy bể.
giờ sẽ đầy bể.
Do đó, trong một giờ, hai vòi cùng chảy được số phần bể là: ![]() (bể).
(bể).
Trong 1 giờ, vòi thứ nhất chảy được ![]() (bể), vòi thứ hai chảy được
(bể), vòi thứ hai chảy được ![]() (bể).
(bể).
Ta có phương trình: ![]()
Nếu mở vòi thứ nhất chảy trong 10 phút và vòi thứ hai chảy trong 12 phút thì đầy ![]() bể nên ta có phương trình
bể nên ta có phương trình ![]()
Từ ![]() và
và ![]() ta có hệ phương trình
ta có hệ phương trình  .
.
Từ phương trình thứ nhất, ta có: ![]() , thế vào phương trình thứ hai, ta được:
, thế vào phương trình thứ hai, ta được:
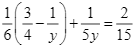
![]()
![]()
![]()
![]() (TMĐK).
(TMĐK).
Thay ![]() vào hệ phương trình thứ nhất, được
vào hệ phương trình thứ nhất, được ![]() suy ra
suy ra ![]() (TMĐK).
(TMĐK).
Vậy vòi thứ nhất chảy một mình đầy bể trong 2 giờ, vòi thứ hai chảy một mình đầy bể trong 4 giờ.
Lời giải
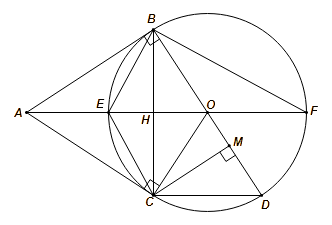
Theo câu a, ![]() (g.g), suy ra
(g.g), suy ra ![]() .
.
Suy ra ![]() .
.
Do đó, ![]() hay
hay ![]()
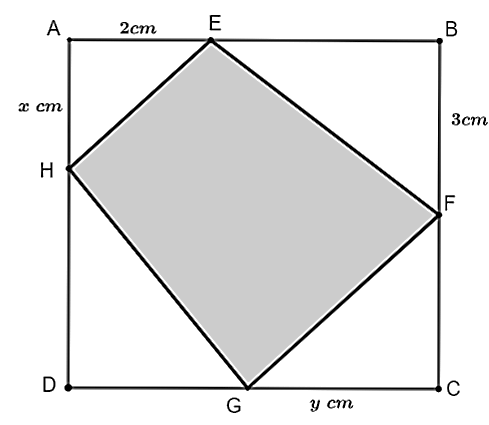
Xét ![]() vuông tại
vuông tại ![]() , có:
, có: ![]()
Suy ra 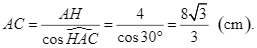
Xét ![]() vuông tại
vuông tại ![]() , có:
, có: ![]()
Diện tích hình quạt giới hạn bởi các bán kính ![]() và cung nhỏ
và cung nhỏ ![]() là:
là:
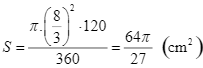 .
.
Vậy diện tích hình quạt giới hạn bởi các bán kính ![]() và cung nhỏ
và cung nhỏ ![]() là
là ![]()
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.