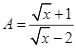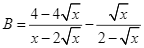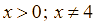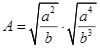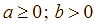Câu hỏi:
17/12/2024 377
Giải bài toán sau bằng cách lập hệ phương trình.
Hai vòi nước cùng chảy vào một bể không có nước thì sau 1 giờ 20 phút sẽ đầy. Nếu mở vòi thứ nhất chảy trong 10 phút và vòi thứ hai chảy trong 12 phút thì đầy 
bể. Hỏi mỗi vòi chảy một mình thì sau bao lâu mới đầy bể?
Giải bài toán sau bằng cách lập hệ phương trình.
Hai vòi nước cùng chảy vào một bể không có nước thì sau 1 giờ 20 phút sẽ đầy. Nếu mở vòi thứ nhất chảy trong 10 phút và vòi thứ hai chảy trong 12 phút thì đầy bể. Hỏi mỗi vòi chảy một mình thì sau bao lâu mới đầy bể?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi 
(giờ) là thời gian để vòi thứ nhất chảy một mình đầy bể;
(giờ) là thời gian để vòi thứ hai chảy một mình đầy bể (
).
Đổi: 1 giờ 20 phút = 
giờ, 12 phút = 
giờ, 10 phút = 
giờ.
Theo đề, hai vòi cùng chảy thì sau giờ sẽ đầy bể.
Do đó, trong một giờ, hai vòi cùng chảy được số phần bể là: 
(bể).
Trong 1 giờ, vòi thứ nhất chảy được 
(bể), vòi thứ hai chảy được 
(bể).
Ta có phương trình: 
Nếu mở vòi thứ nhất chảy trong 10 phút và vòi thứ hai chảy trong 12 phút thì đầy 
bể nên ta có phương trình 
Từ 
và 
ta có hệ phương trình 
.
Từ phương trình thứ nhất, ta có: 
, thế vào phương trình thứ hai, ta được:
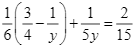
(TMĐK).
Thay vào hệ phương trình thứ nhất, được 
suy ra 
(TMĐK).
Vậy vòi thứ nhất chảy một mình đầy bể trong 2 giờ, vòi thứ hai chảy một mình đầy bể trong 4 giờ.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
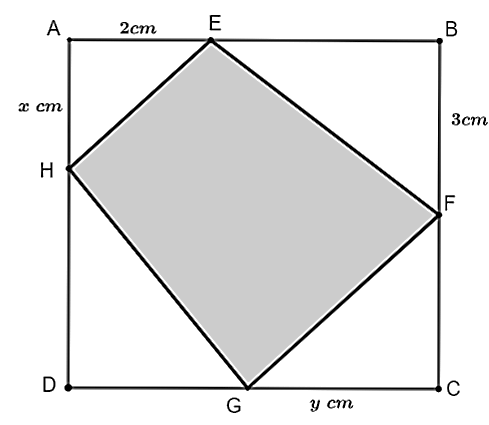
Với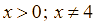 
, ta có: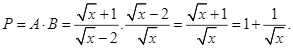 
Với 
để 
nhận giá trị nguyên thì 
là nhận giá trị nguyên hay 
.
Do đó, 
là ước của 
Mà 
nên 
hay 
(thỏa mãn).
Vậy thì nhận giá trị nguyên.
Lời giải
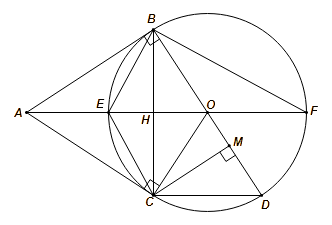
Theo câu a, 
(g.g), suy ra 
.
Suy ra 
.
Do đó, 
hay 
Xét 
vuông tại 
, có: 
Suy ra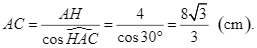 
Xét 
vuông tại 
, có: 
Diện tích hình quạt giới hạn bởi các bán kính 
và cung nhỏ 
là:
.
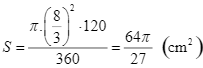Vậy diện tích hình quạt giới hạn bởi các bán kính và cung nhỏ là 
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1
-
Chuyên đề 8: Hình học (có đáp án)