Câu hỏi:
23/12/2024 630
Cho hai điện tích điểm \({q_1} = 6\mu {\rm{C}}\) và \({q_2} = 54\mu {\rm{C}}\) đặt tại hai điểm A, B trong không khí cách nhau 6 cm. Sau đó người ta đặt một điện tích q3 tại điểm C.
a) Xác định vị trí điểm C để điện tích q3 nằm cân bằng.
b) Xác định dấu và độ lớn của q3 để cả hệ cân bằng.
Cho hai điện tích điểm \({q_1} = 6\mu {\rm{C}}\) và \({q_2} = 54\mu {\rm{C}}\) đặt tại hai điểm A, B trong không khí cách nhau 6 cm. Sau đó người ta đặt một điện tích q3 tại điểm C.
a) Xác định vị trí điểm C để điện tích q3 nằm cân bằng.
b) Xác định dấu và độ lớn của q3 để cả hệ cân bằng.
Câu hỏi trong đề: 14 bài tập Chủ đề 3. Điện trường có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Do \({q_1}{q_2} > 0\), nên để q3 cân bằng thì q3 phải nằm trong đoạn AB.
Ta có: \({\overrightarrow F _3} = {\overrightarrow F _{13}} + {\overrightarrow F _{23}} = \vec 0\).
\( \Rightarrow {F_{13}} = {F_{23}} \Leftrightarrow k\frac{{\left| {{q_1}{q_3}} \right|}}{{A{C^2}}} = k\frac{{\left| {{q_2}{q_3}} \right|}}{{B{C^2}}} \Leftrightarrow \frac{6}{{A{C^2}}} = \frac{{54}}{{B{C^2}}} \Leftrightarrow 3AC - BC = 0.\)
Mà \(AC + BC = AB = 6{\rm{\;cm}} \Rightarrow AC = 1,5{\rm{\;cm}}\) và \(BC = 4,5{\rm{\;cm}}{\rm{.}}\)
Vậy điểm C cách điểm A và B lần lượt là 1,5 cm và 4,5 cm.
b) Vì \({q_1}{q_2} > 0\), nên lực tác dụng lên q2 là lực đẩy. Vậy để hệ cân bằng thì \({q_3} < 0\).
\({F_{12}} = {F_{32}} \Leftrightarrow k\frac{{\left| {{q_1}{q_2}} \right|}}{{A{B^2}}} = k\frac{{\left| {{q_2}{q_3}} \right|}}{{B{C^2}}} \Leftrightarrow \frac{{\left| {{q_1}} \right|}}{{A{B^2}}} = \frac{{\left| {{q_3}} \right|}}{{B{C^2}}}\)
\( \Rightarrow \left| {{q_3}} \right| = \left| {{q_1}} \right|\frac{{B{C^2}}}{{A{B^2}}} = 6 \cdot {\left( {\frac{{4,5}}{6}} \right)^2} = 3,375\mu {\rm{C}}\). Vậy điện tích của q3 là \( - 3,375\mu {\rm{C}}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Điện thế tại M là \({V_M} = \frac{{{W_d}}}{q} = \frac{{ - {{32.10}^{ - 19}}}}{{ - 1,{{6.10}^{ - 19}}}} = 20V\). Chọn C.
Lời giải
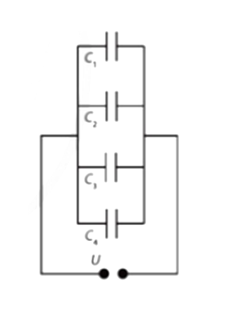
a) \({C_{td}} = {C_1} + {C_2} + {C_3} = 3 + 6 + 12 + 24 = 45,0\mu {\rm{F}}\).
b) \({Q_3} = {C_3}U = 12.18 = 216\mu {\rm{C}}\)
c) \({Q_{td}} = {C_{td}}.U = 45.18 = 810\,\mu {\rm{C}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Trưng Yên - Hưng Yên có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 6)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận