Giải tam giác nhọn ABC biết AB = 2,1; AC = 3,8 và \(\widehat B = 70^\circ \). (Kết quả độ dài các cạnh làm tròn đến hàng phần mười, góc làm tròn đến độ)
Câu hỏi trong đề: 12 bài tập Giải tam giác vuông có lời giải !!
Quảng cáo
Trả lời:
Hướng dẫn giải
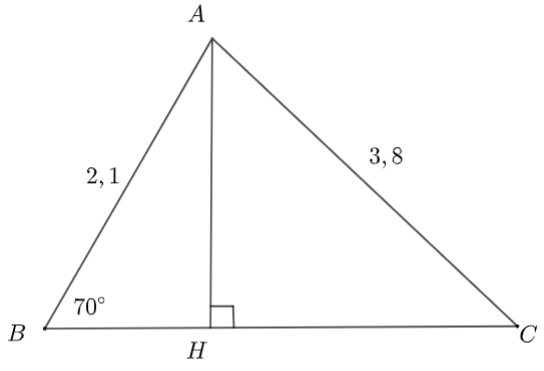
Kẻ AH vuông góc với BC tại H.
Xét tam giác BHA vuông tại H, ta có:
AH = sin 70°.AB = sin 70°.2,1 ≈ 2.
BH = cos 70°.AB = cos 70°.2,1 ≈ 0,7.
Xét tam giác HAC vuông tại H, ta có:
sinC = \(\frac{{AH}}{{AC}} = \frac{2}{{3,8}}\) suy ra \(\widehat C \approx 32^\circ \).
HC = cosC.AC = cos 32°. 3,8 ≈ 3,2.
Do đó, BC = BH + HC = 3,2 + 0,7 = 3,9 cm.
Xét tam giác ABC, ta có: \(\widehat {BAC} = 180^\circ - \left( {\widehat B + \widehat C} \right) = 180^\circ - \left( {70^\circ + 32^\circ } \right) = 78^\circ \)
Vậy BC = 3,9 cm và \(\widehat {BAC} = 78^\circ \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
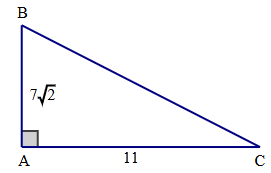
Ta có: tanB = \(\frac{{AC}}{{AB}} = \frac{{11}}{{7\sqrt 2 }}\) = 1,1145.
Suy ra \(\widehat B = 48^\circ \).
Lại có \(\widehat B + \widehat C = 90^\circ \) suy ra \(\widehat C = 42^\circ \).
Áp dụng định lí Pytagore vào tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 = (\(7\sqrt 2 \))2 + 112 = 219.
Suy ra \(BC = \sqrt {219} \approx 14,8\) cm.
Lời giải
Hướng dẫn giải
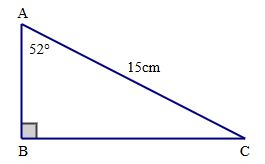
Ta có: ABC vuông tại B.
Suy ra \(\widehat A + \widehat C = 90^\circ \).
Mà \(\widehat A = 52^\circ \) suy ra \(\widehat C = 38^\circ \).
Ta có: AB = AC.sinC = 15.sin38° ≈ 9,2 cm.
BC = AC.sinA = 15.sin52° ≈ 11,8 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.