Câu hỏi:
14/01/2025 3,939
Một con lắc di chuyển từ A đến vị trí B (Hình vẽ). Tính độ dài quãng đường AB mà con lắc đó đã di chuyển, biết rằng dợi dây OA có độ dài l = 2 (cm) và tia OA tạo với phương thẳng đứng góc α = 15°
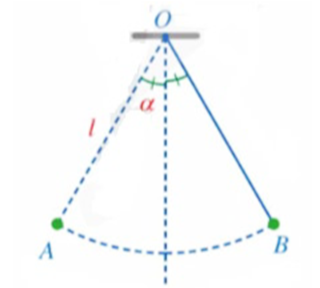
Một con lắc di chuyển từ A đến vị trí B (Hình vẽ). Tính độ dài quãng đường AB mà con lắc đó đã di chuyển, biết rằng dợi dây OA có độ dài l = 2 (cm) và tia OA tạo với phương thẳng đứng góc α = 15°
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: \(\widehat {AOB} = 2\alpha = 2.15^\circ = 30^\circ \) là số đo của cung AB.
Độ dài quãng đường AB mà con lắc đó đã di chuyển là:
l = \(\frac{{\pi Rn}}{{180}} = \frac{{\pi 2.30}}{{180}} = \frac{\pi }{3}\) (cm)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Diện tích hình quạt đó là: l = \(\frac{{\pi {{.2}^2}.150}}{{360}} = \frac{{5\pi }}{3}\) (dm).
b) Ta có: \(S = \frac{{lR}}{2}\) suy ra l = \(\frac{{2S}}{R} = \frac{{2.\frac{{5\pi }}{3}}}{2} = \frac{{5\pi }}{3}\) (dm).
Vậy độ dài cung tương ứng với hình quạt đó là: \(\frac{{5\pi }}{3}\) dm.
Lời giải
Hướng dẫn giải
Đổi 1 dặm = 1 609 m = 1,609 km.
Diện tích vùng biển có thể nhìn thấy ánh sáng từ hải đăng là:
S = \(\frac{{{{\left( {18.1,609} \right)}^2}.245\pi }}{{360}} \approx 1793\) (km2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận