Ở huyện Đông Anh, Hà Nội, vào tháng 7, người ta đo được xác suất để có mưa vào thứ hai là 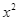 . Nếu trời có mưa vào thứ hai thì xác suất để có mưa vào thứ ba là
. Nếu trời có mưa vào thứ hai thì xác suất để có mưa vào thứ ba là 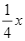 . Nếu thứ hai không có mưa thì xác suất để có mưa vào thứ ba là
. Nếu thứ hai không có mưa thì xác suất để có mưa vào thứ ba là 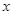 .
.
a) Biểu thức theo biến 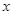 cho biết xác suất để mưa sẽ rơi vào cả thứ hai và thứ ba là
cho biết xác suất để mưa sẽ rơi vào cả thứ hai và thứ ba là 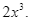
b) Khả năng trời sẽ có mưa vào cả thứ hai và thứ ba là 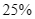 khi
khi 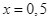 .
.
c) Biểu thức theo biến 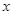 , cho biết xác suất để trời sẽ mưa vào thứ ba là
, cho biết xác suất để trời sẽ mưa vào thứ ba là 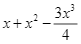 .
.
d) Xác suất để có mưa vào thứ hai với điều kiện của biến 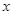 thỏa mãn xác suất trời sẽ mưa vào thứ ba lớn nhất bằng
thỏa mãn xác suất trời sẽ mưa vào thứ ba lớn nhất bằng 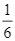 .
.
Ở huyện Đông Anh, Hà Nội, vào tháng 7, người ta đo được xác suất để có mưa vào thứ hai là ![]() . Nếu trời có mưa vào thứ hai thì xác suất để có mưa vào thứ ba là
. Nếu trời có mưa vào thứ hai thì xác suất để có mưa vào thứ ba là ![]() . Nếu thứ hai không có mưa thì xác suất để có mưa vào thứ ba là
. Nếu thứ hai không có mưa thì xác suất để có mưa vào thứ ba là ![]() .
.
a) Biểu thức theo biến ![]() cho biết xác suất để mưa sẽ rơi vào cả thứ hai và thứ ba là
cho biết xác suất để mưa sẽ rơi vào cả thứ hai và thứ ba là ![]()
b) Khả năng trời sẽ có mưa vào cả thứ hai và thứ ba là ![]() khi
khi ![]() .
.
c) Biểu thức theo biến ![]() , cho biết xác suất để trời sẽ mưa vào thứ ba là
, cho biết xác suất để trời sẽ mưa vào thứ ba là ![]() .
.
d) Xác suất để có mưa vào thứ hai với điều kiện của biến ![]() thỏa mãn xác suất trời sẽ mưa vào thứ ba lớn nhất bằng
thỏa mãn xác suất trời sẽ mưa vào thứ ba lớn nhất bằng ![]() .
.
Quảng cáo
Trả lời:
Gọi biến cố ![]() là: “Có mưa vào thứ hai”; biến cố
là: “Có mưa vào thứ hai”; biến cố ![]() là: “Có mưa vào thứ ba”.
là: “Có mưa vào thứ ba”.
Từ giả thiết có ![]() ;
;
![]() và
và ![]() .
.
a) Sai. Ta có 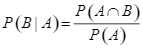 . Suy ra
. Suy ra ![]() .
.
Xác suất để mưa sẽ rơi vào cả thứ hai và thứ ba là ![]() .
.
b) Sai. Để khả năng trời sẽ có mưa vào cả thứ hai và thứ ba là ![]() thì
thì ![]() .
.
c) Sai. Xác suất để trời sẽ mưa vào thứ ba là
![]()
![]()
![]() .
.
d) Đúng. Điều kiện của biến ![]() .
.
Xét hàm số ![]() trên đoạn
trên đoạn ![]() . Ta có
. Ta có 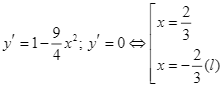 .
.
![]() Suy ra
Suy ra ![]() .
.
Như vậy, khi ![]() thì xác suất trời sẽ mưa vào thứ ba là lớn nhất.
thì xác suất trời sẽ mưa vào thứ ba là lớn nhất.
Theo công thức Bayes, xác suất để có mưa vào thứ hai biết trời mưa vào thứ ba là
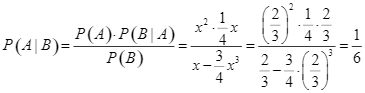 .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 0,33.
|
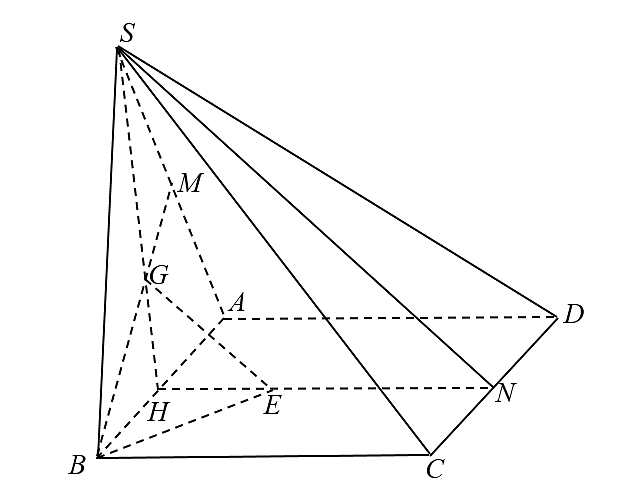
Gọi Do Trong mặt phẳng Ta có
|
|
Do ![]() là trọng tâm của tam giác
là trọng tâm của tam giác ![]() nên
nên 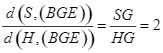
![]() .
.
Ta có ![]() nên
nên ![]() .
.
Thể tích của tứ diện ![]() là
là ![]() .
.
Mặt khác ![]() .
.
Ta có ![]() ,
, ![]() ,
,
 .
.
Vì ![]() nên tam giác
nên tam giác ![]() vuông tại
vuông tại ![]() ,
, ![]() .
.
Do đó ![]() . Vậy
. Vậy 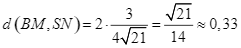 .
.
Lời giải
Ta có ![]() .
.
a) Sai. Ta có
![]()
Dấu đẳng thức xảy ra khi ![]() .
.
Vậy tiếp tuyến có hệ số góc nhỏ nhất của đồ thị hàm số ![]() là tiếp tuyến tại điểm
là tiếp tuyến tại điểm ![]() có phương trình là
có phương trình là ![]() nên tiếp tuyến không đi qua điểm
nên tiếp tuyến không đi qua điểm ![]() .
.
b) Sai. Hàm số ![]() liên tục trên
liên tục trên ![]() .
.
Giải 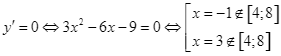 .
.
Ta có ![]() .
.
c) Đúng. Ta có: ![]() . Giải
. Giải ![]() nên tọa độ tâm đối xứng của đồ thị hàm số đã cho là
nên tọa độ tâm đối xứng của đồ thị hàm số đã cho là ![]() .
.
d) Đúng. Đồ thị hàm số có 2 điểm cực trị là ![]() .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.